- csprimer-computersystem-concept3
- Programming C
- Explanation:
- Example:
- 🔢 What is
0xffffffff? - 🧠 Signed vs Unsigned Int in C
- ⚙️ Two’s Complement Concept
- ✅ Why
0xffffffff= -1 in signed int - 🚫 Why the Loop Breaks
- Summary
- 🔍 What does it do?
- 🔥 Why is it faster?
- 🧠 Example:
n = 0b10110000 - 💡 Why
n & (n - 1)clears the lowest set bit? - Summary:
- 🧠 What is
popcnt? - ✅ Why your teacher used
-march=nativeand-O3 - 🧩 What does the assembly mean?
- 🚀 Summary
- 🧠 The Core Idea: Parallel Byte Aggregation
- ⚡ Example: Parallel 16-bit Pairing
- 🚀 In SIMD Hardware:
- 🧪 Summary:
- 🧰 Python can’t truly do this in parallel, but…
- 🧠 What Is a Divide and Conquer Algorithm?
- ✅ Classic Examples
- 🧮 For Byte Summing?
- 👇 In simple Python example:
- Script Breakdown
- Example Usage
- Why It Can Be Used for Speed Testing (Profiling)
- How It Acts Like a Profiler
- Example Scenario
- Limitations
- Improvements for Better Profiling
- Conclusion
- Overview of the Program
- Code Breakdown
- How It Fits with the Bash Script
- Key C Concepts for Beginners
- Example: Completing
ispangram - Running the Program
- Sample Run
- Why This Code?
- Next Steps
- the different C compiler , gcc vs clang
- Key Features of
<stdint.h>- 1. Arrays and Pointers in C
- 2. Array Indexing:
arr[3] - 3. Pointer Arithmetic:
*(arr + 3) - 4. Why
arr[3]==*(arr + 3)? - 5. Example from Your Code
- 6. What Your Teacher Is Teaching
- 7. Key Takeaways
- 8. A Visual Explanation
- 9. Practice to Reinforce
- 1. Preprocessor Directives
- 2. Conditional Compilation
- 3. The Role of the
DEBUGMacro - 4. The
fprintf(stderr, "error\n")Line - 5. Why This Matters
- 6. Fixing the Code
- 7. How
DEBUGIs Set - 8. Example Compilation Scenarios
- 9. Broader Lesson
- 10. Practice to Reinforce
- 11. Connection to Pointers (from Your Previous Question)
- 1. Overview of Structs in C
- 2. Key Concepts Your Teacher Is Teaching
- 3. Memory Address Calculation:
0x7ffe6b1f9ea0to0x7ffe6b1f9eb8 - 4. Broader Lessons from Your Teacher
- 5. Practice to Reinforce
- 6. Key Takeaways
- Context Setup
- 1.
(int*)b2.value - 2.
*(int*)b2.value - Key Difference
- Why This Happens
- Correct Approach
- Summary
- 🧠 What Your Teacher Is Teaching:
- 🔍 Stack Memory Layout (Key Idea)
- 💥 Why Overwriting Happens:
- ✅ What Your Teacher’s Trying to Teach:
- 🧪 Why This Is “A Small Chance” Case
- 🧠 Takeaway Message:
- 📦 What Is the Stack?
- 📐 Key Characteristics of the Stack
- 🧱 Stack Frame Layout (per function call)
- 🧪 Example: Stack Frame Visualization
- 🤯 Why Memory Bugs Happen
- 🎯 What Your Teacher Is Demonstrating
- 🛡️ Tools to Catch These Bugs
- 👣 Summary
- 🧠 What Is
$rsp? - 🔍 What Does This Do?
- 📐 Why It’s Useful
- 🔧 Try It Yourself
- 🧭 Summary
- 🧠 1.
int x = 5;→ What happens? - 📦 2. What about
&x(the address of x)? - 🧠 3. Visualizing
x,y, andz - 📍 Why This Matters
- 🔄 Address Arithmetic Note
- ✅ TL;DR
- 🔍 What is a
void*? - ❌ Pointer Arithmetic Is Not Allowed on
void*(in C) - 🧠 Why Cast to
char*oruint8_t*? - ✅ Summary
- 🔁 What Is a Cast?
- 🧠 Two Main Kinds of Casts
- ⚠️ Why Casts Are Powerful (and Dangerous)
- 🧰 Common Use Cases
- 👎 What You Should Not Do
- 🧠 Cast vs Implicit Conversion
- 🎯 TL;DR Summary
- 🧠 What Is
void **? - ✅ Real Use Case: Generic Memory Setters
- 🧩 Applying to Your Teacher’s Diagram
- 🚨 Why Is This Confusing?
- 🧠 What’s the Takeaway? - 🧠 Part 1: What Does
void* arr;Mean? - 🔁 Now What If You Usevoid** arr;? - ✅ Your Case: Dynamic Array (Generic) - 📦 Example Use Case -void* arr(raw block of memory): -void** arr(array of pointers): - 🔧 So What Is Your Teacher Trying to Do? - 🔍 Final Analogy
- Key Features of
csprimer-computersystem-concept5
csprimer-computersystem-concept3
NASM Tutorial
hackclub/some-assembly-required: 📖 An approachable introduction to Assembly.

- there is two common x64 , inter and att (linux prefer) push → pushq → push to queue
att: movq , movb (b for byte), bl → long byte
movq , q for qute word quart word → 64 bit → quart of 64 , 16
-
subq: substracting 16 from %rsp
-
operator order is difference btw att and intel
-
look at the construction
one text section , loaded in the memory
Programming C
learn x in y minutes C, Go - Hyperpolyglot read c code , linux source code
- high level of struct
- compile , c knowledge with machine
hello world in c :
int main() {} → why int a linux culture → 0 mean successful like work && run bash order
if return 1; → not , it will not run as successful, can && after
return -1 → assertion fail → fail reminder in terminal
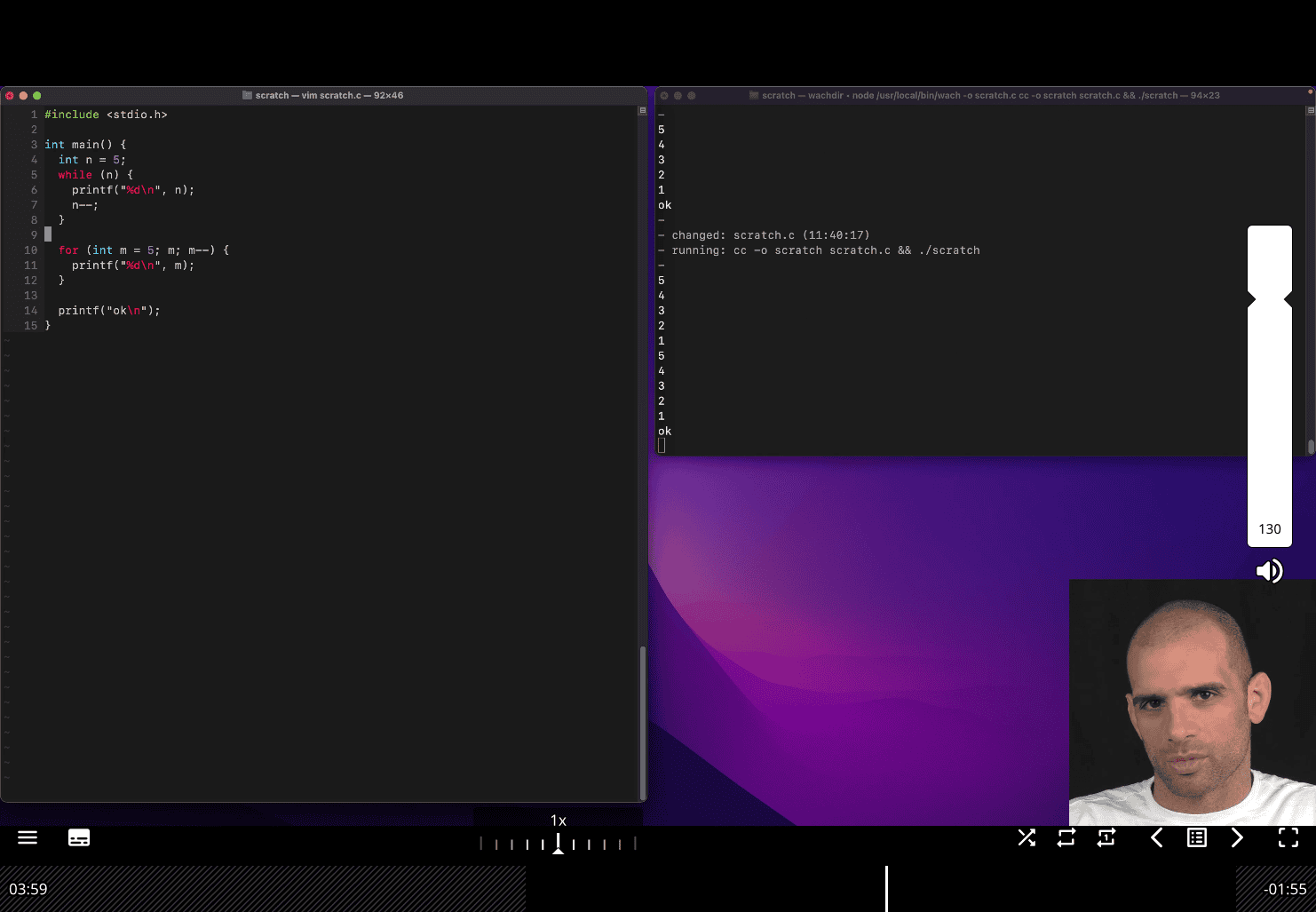
int bitcount(int n) { int count = 0; while (n){
} }
in c , 0 mean true , 1 → false
- don’t have boolean in c , so using
while(n)-> keep runing while n is not 0
n & 0x01 is a bitwise AND operation that checks whether the least significant bit (LSB) of n is 1 or 0.
Explanation
0x01is hexadecimal for00000001in binary.n & 0x01comparesnwith00000001using bitwise AND:- If the LSB of
nis1, the result is1. - If the LSB is
0, the result is0.
- If the LSB of
Example
n = 5; // binary: 0101
n & 0x01 = 1 // because the LSB is 1This is commonly used to count the number of 1s in a binary number (also known as the Hamming weight or population count).
Also, your function is missing a return statement. Here’s the corrected version:
int bitcount(int n) {
int count = 0;
while (n) {
if (n & 0x01) {
count += 1;
}
n >>= 1;
}
return count;
}Let me know if you want a version that’s more efficient.
as there is only 1 and 0 out there , so if there is 1 in the lsb , least significant bit → shift right until 0

int bitcount(int n) { int count = 0; while (n) { count += n & 0x01; n >>= 1; } return count; }
-
refactor as 0 dont affect count, add them all in here lol
int main() { assert(bitcount(0) == 0); assert(bitcount(1) == 1); assert(bitcount(3) == 2); assert(bitcount(8) == 1); // harder case: assert(bitcount(0xffffffff) == 32); printf("OK\n"); }
assert(bitcount(0xffffffff) == 32); this break the while(n) loop , so the n != 0 for 0xffffffff
🔢 What is 0xffffffff?
In binary, 0xffffffff is:
11111111 11111111 11111111 11111111 // 32 bits
That’s all bits set to 1 — which equals 4294967295 in unsigned interpretation.
🧠 Signed vs Unsigned Int in C
intis signed (can represent negative and positive numbers).- It uses two’s complement representation to handle negatives.
⚙️ Two’s Complement Concept
In two’s complement, the highest bit (leftmost bit) is the sign bit:
0xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx→ positive1xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx→ negative
To get the negative value of a binary number:
- Invert all the bits
- Add 1
So in 32-bit signed int:
0x00000001→ 10x7fffffff→ 2,147,483,647 (max signed int)0x80000000→ -2,147,483,648 (min signed int)0xffffffff→ -1
✅ Why 0xffffffff = -1 in signed int
Let’s apply two’s complement:
0xffffffff=11111111 11111111 11111111 11111111- Invert:
00000000 00000000 00000000 00000000 - Add 1:
00000000 00000000 00000000 00000001→ that’s1 - So original =
-1
Hence, 0xffffffff is interpreted as -1 in a signed int.
🚫 Why the Loop Breaks
Right-shifting signed -1:
-1 >> 1→ still-1, because the sign bit (1) is preserved.- So
nnever becomes0, andwhile (n)becomes infinite loop.
Summary
| Hex | Binary (32-bit) | Interpreted as |
|---|---|---|
0xffffffff | 11111111 11111111 11111111 11111111 | -1 (signed int) |
4294967295 (unsigned int) |
So: same bits, different meaning depending on signed vs unsigned.
Let me know if you’d like a visual to reinforce this!
int bitcount(unsigned n) { int count = 0; while (n) { count += n & 0x01; n >>= 1; } return count; }
int n → unsigned → fixed

before using belew , it loop 32 times for case 0xfff … == 32
- x & x-1 → deleted the rightmost bit of x using bitwise &
 Excellent question — this is a classic bit manipulation trick often called Brian Kernighan’s Algorithm.
Excellent question — this is a classic bit manipulation trick often called Brian Kernighan’s Algorithm.
🔍 What does it do?
This line:
n &= (n - 1);clears the lowest set bit (the rightmost 1) in n.
Each time this happens, we increment count.
So instead of looping through all 32 bits, we loop only through the number of set bits.
🔥 Why is it faster?
Let’s compare with your previous method:
Previous method
while (n) {
count += n & 1;
n >>= 1;
}- Always does up to 32 iterations, checking each bit one-by-one.
New method
while (n) {
n &= (n - 1);
count++;
}- Does only as many iterations as there are 1s in
n.
🧠 Example: n = 0b10110000
Set bits: 3 Old loop → 8 iterations New loop → 3 iterations ✔️
💡 Why n & (n - 1) clears the lowest set bit?
Let’s take an example:
n = 0b10110000
n - 1 = 0b10101111
---------------------
n & (n-1)= 0b10100000 ← rightmost 1 cleared
So each iteration removes one 1, getting us closer to 0 faster.
Summary
| Method | Iterations Needed | Performance Benefit |
|---|---|---|
n >>= 1 | Up to 32 | Slower for sparse bits |
n &= (n-1) | Only set bits (Hamming weight) | Faster overall |
Your teacher’s version is more efficient, especially when n has few set bits. It’s a smart use of bitwise logic.
advanced C : compiler →
pop count (compiler) population count
cc -O3 -fomit-frame-pointer -march=native -c bitcount.c
objdump -d bitcount.o
🧠 What is popcnt?
popcntis a CPU instruction that counts the number of1bits (set bits) in a binary number.- It’s built into modern CPUs (like Intel and AMD).
- It’s extremely fast — much faster than any loop.
Think of it as a “hardware-accelerated bitcount.”
✅ Why your teacher used -march=native and -O3
-O3: Tells the compiler to fully optimize the code.-march=native: Allows the compiler to use CPU-specific features, likepopcnt.
So when the compiler sees your function:
int bitcount(unsigned n) {
int count = 0;
while (n) {
n &= (n-1);
count++;
}
return count;
}Instead of compiling a loop, it says:
“Oh! This is just a popcount — I’ll replace it with the
popcntinstruction.”
🧩 What does the assembly mean?
0: 31 c0 xor %eax, %eax // set EAX = 0 (clear return value register)
2: f3 0f b8 c7 popcnt %edi, %eax // EAX = popcount(EDI)
6: c3 ret // return
Let’s break it down:
| Assembly | Meaning |
|---|---|
xor %eax, %eax | Clear the eax register (set to 0) |
popcnt %edi, %eax | Count bits in edi and put result in eax |
ret | Return from function |
Registers:
%edi: where the first argument (unsigned n) is passed (in 64-bit calling convention).%eax: where the return value is stored.
🚀 Summary
- The compiler recognized your bitcount function and replaced it with a single fast
popcntCPU instruction. - This is only possible with optimization flags (
-O3 -march=native) and on CPUs that supportpopcnt.
So this is your teacher showing you:
“Writing clever code is cool, but modern compilers and CPUs can do even better!”
Let me know if you want a visual of how registers or popcnt work internally.
adding inline compiler wtf
#include <nmintrin.h>
__builtin_popcount(n) Counts 1-bits efficiently <nmmintrin.h> Enables SSE4.2 intrinsics like popcnt Replaces manual loop Cleaner, faster, compiler-optimized
- using mechine code instruction → more optimize
as it is usign mechine instruction , not all computer have popcount , so if compile didn’t set to march = native , it will just use other assembly way
no loop in in the assembly
primer suggesting this book:
Hacker’s Delight
there is counting tips about bitw
Parallel way to count the bit from pair
32 → 16 → 4 → 2 pair 2 bit and sum
I am not gpt genthis right in below
Ah! If your teacher mentioned that the algorithm allows you to “run in parallel,” then he’s likely referring to an approach inspired by SIMD-style or parallel prefix sum techniques.
🧠 The Core Idea: Parallel Byte Aggregation
When decoding a multi-byte little-endian number (e.g. a4 01 00 00), the normal method is sequential:
value = b[0] + (b[1] << 8) + (b[2] << 16) + (b[3] << 24)This is inherently sequential because each shift depends on the byte’s position.
But with parallel processing, you can:
- Split the bytes into groups (e.g. 2-byte chunks)
- Perform operations on those chunks in parallel
- Combine the partial results later
⚡ Example: Parallel 16-bit Pairing
Let’s say you have 4 bytes:
bs = [a4, 01, 00, 00]
Instead of:
a4 + 01 << 8 + 00 << 16 + 00 << 24You could do:
-
Group into 2-byte chunks:
chunk1 = a4 01 => little-endian: 0x01a4 chunk2 = 00 00 => 0x0000 -
Then compute:
value = chunk1 + (chunk2 << 16)
You’re now doing fewer additions, and this structure can be parallelized in low-level or SIMD hardware (e.g., SSE/AVX).
🚀 In SIMD Hardware
On CPUs that support SIMD (like Intel with AVX), operations like “multiply and accumulate” or “shift and add” on multiple 16- or 32-bit integers can be vectorized, meaning done in parallel registers.
Even in GPU programming (CUDA, OpenCL), this matters.
🧪 Summary
Your teacher is hinting at an algorithm that makes endian conversion more parallel-friendly:
| Feature | Explanation |
|---|---|
| ✅ Break into 2-byte chunks | Reduces loop iterations |
| ✅ SIMD-friendly | You can shift/add in parallel lanes |
| ✅ More efficient for large arrays | Works well in image or video data |
| ✅ CPU/GPU optimization | Used in compilers and video codecs |
🧰 Python can’t truly do this in parallel, but
You could simulate the logic and understand how it reduces dependency per byte.
Want me to show you this idea with an example that compares standard vs 2-byte parallel-style summing in Python?
Ah! You’re thinking of Divide and Conquer algorithms. (That’s the correct spelling 😊)
🧠 What Is a Divide and Conquer Algorithm?
Divide and Conquer is a strategy to solve complex problems by:
- Divide — Breaking the problem into smaller subproblems.
- Conquer — Solving each subproblem recursively (or in parallel).
- Combine — Merging the solutions of subproblems to get the final answer.
✅ Classic Examples
| Problem | How Divide & Conquer Works |
|---|---|
| Merge Sort | Divide the array, sort both halves recursively, then merge the sorted halves |
| Quick Sort | Partition the array, then sort left and right parts recursively |
| Binary Search | Divide search space in half each time |
| Fast Fourier Transform (FFT) | Split signals, apply FFT recursively, then combine frequency results |
| Matrix Multiplication (Strassen) | Break matrix into quadrants, multiply submatrices recursively |
🧮 For Byte Summing?
Yes — your teacher might be suggesting a Divide and Conquer approach to summing bytes, like:
- Pair 2 bytes together and form small integers
- Sum pairs recursively
- Combine results
This lets you parallelize the summing, especially if:
- You’re reading huge binary files
- You’re processing pixels or data blocks
- You’re optimizing for SIMD/CPU threads
👇 In simple Python example
def le_dc(bs): # Divide and Conquer for little-endian bytes
if len(bs) == 1:
return bs[0]
mid = len(bs) // 2
left = le_dc(bs[:mid])
right = le_dc(bs[mid:])
return left + (right << (8 * mid))Same result as the loop-based method, but this can be done in parallel in theory, because left and right are independent until the final shift + add.
Would you like a visual animation or simple diagram of how this divide-and-conquer version works compared to normal summing?
- primer mention : What Is a Divide and Conquer Algorithm?
Divide and Conquer is a strategy to solve complex problems by:
Divide — Breaking the problem into smaller subproblems.
Conquer — Solving each subproblem recursively (or in parallel).
Combine — Merging the solutions of subproblems to get the final answer.
Let’s break down the provided Bash script and explain its functionality, focusing on how it can be used for speed testing (profiling) in a Unix environment.
Script Breakdown
#!/usr/bin/env bash- Shebang: Specifies that the script should be executed using the Bash interpreter found in the user’s environment path. Using
/usr/bin/env bashensures portability across systems where Bash might be installed in different locations.
set -euo pipefail- Shell Options:
-e: Exits immediately if any command fails (non-zero exit status).-u: Treats unset variables as errors and exits.-o pipefail: Ensures that a pipeline fails if any command in the pipeline fails, not just the last one.
- Purpose: These settings make the script robust by catching errors early and preventing unexpected behavior.
IFS=$'\n\t'- Internal Field Separator (IFS): Sets the field separator to newline (
\n) and tab (\t). This controls how Bash splits words during command substitution and loops, ensuring that spaces in input/output are preserved correctly. - Purpose: Prevents issues when handling file contents or arguments with spaces.
trap "kill 0" SIGINT- Trap: Sets up a signal handler for
SIGINT(e.g., when the user pressesCtrl+C). The commandkill 0sends the signal to all processes in the current process group, effectively terminating the script and any child processes it spawned. - Purpose: Ensures clean termination of the script and its subprocesses when interrupted.
if [[ "$#--1-|" < 1 ]]; then
echo "Usage: ./test.sh cmd" >&2
exit 1
fi- Argument Check:
$#: Number of command-line arguments passed to the script.- If fewer than 1 argument is provided, it prints a usage message to stderr (
>&2) and exits with status1(indicating an error).
- Purpose: Ensures the script is called with at least one argument (the command to test).
diff <(cat cases.txt | eval "(time $@)") pangrams.txt- Main Command:
cat cases.txt: Reads the contents ofcases.txt(presumably a file containing test inputs, such as strings or pangrams).|: Pipes the output ofcat cases.txtto the next command.eval "(time $@)":$@: Represents all command-line arguments passed to the script (e.g.,python3 some_script.py).time: A Unix utility that measures the execution time of the command that follows.eval: Evaluates the string(time $@)as a command. This allows the script to run the user-provided command (e.g.,python3 some_script.py) with thetimecommand prepended, measuring its execution time.- The parentheses
(...)in theevalensure that thetimeoutput (timing statistics) is captured along with the command’s output.
<(...): Process substitution. The output of the command inside<(...)(i.e., the output ofcat cases.txt | eval "(time $@)") is treated as a temporary file.diff: Compares the output of the command (from process substitution) with the contents ofpangrams.txt(presumably a file containing expected outputs).
- Purpose: Runs the specified command with input from
cases.txt, measures its execution time, and compares its output topangrams.txtto verify correctness.
Example Usage
The script is invoked as:
./test.sh python3 some_script.py- What Happens:
- The script checks that at least one argument (
python3 some_script.py) is provided. - It reads
cases.txt(e.g., containing test inputs like pangrams). - It pipes these inputs to the command
time python3 some_script.py. - The
timecommand measures how longpython3 some_script.pytakes to process the inputs. - The output of
python3 some_script.py(plus thetimecommand’s timing statistics) is compared topangrams.txtusingdiff. - If the outputs match,
diffproduces no output (indicating success). If they differ,diffshows the differences, and the script fails (due toset -e).
- The script checks that at least one argument (
Why It Can Be Used for Speed Testing (Profiling)
The script facilitates speed testing in a Unix environment for the following reasons:
-
Use of
timeCommand:- The
timeutility measures the execution time of the provided command ($@), reporting metrics such as:- Real time: Total wall-clock time from start to finish.
- User time: CPU time spent in user mode.
- System time: CPU time spent in kernel mode.
- These metrics are included in the output, allowing the user to assess the performance of the command (e.g.,
python3 some_script.py).
- The
-
Input/Output Testing:
- The script feeds test inputs from
cases.txtto the command and compares the output topangrams.txt. This ensures that performance is measured while verifying correctness. - By testing with a standardized set of inputs, the script provides a consistent benchmark for comparing the speed of different implementations or optimizations.
- The script feeds test inputs from
-
Automation and Reusability:
- The script automates the process of running a command, measuring its time, and verifying its output. This is ideal for profiling multiple runs or comparing different programs (e.g., different Python scripts or algorithms).
- The use of
$@allows the script to work with any command, making it flexible for testing various executables or scripts.
-
Error Handling:
- The
set -euo pipefailandtrapensure that the script fails gracefully on errors or interruptions, making it reliable for repeated profiling runs. - If the command fails or produces incorrect output, the script exits with an error, alerting the user to issues that might affect performance measurements.
- The
-
Unix Environment Integration:
- The script leverages Unix tools (
time,diff,cat, process substitution) to create a lightweight, portable profiling setup without requiring specialized profiling software. - It fits naturally into a Unix workflow, where piping, redirection, and file-based input/output are common.
- The script leverages Unix tools (
How It Acts Like a Profiler
While not a full-fledged profiler (e.g., it doesn’t provide detailed function-level timing or memory usage like gprof or valgrind), the script serves as a simple performance testing tool by:
- Measuring Execution Time: The
timecommand provides high-level timing metrics, which are useful for comparing the overall performance of different programs or versions of a program. - Standardized Testing: By using fixed input (
cases.txt) and expected output (pangrams.txt), it ensures fair comparisons across runs. - Correctness Verification: The
diffcommand ensures that performance is measured only for correct outputs, preventing misleading results from faulty implementations. - Ease of Use: It simplifies the process of running timed tests, making it accessible for quick benchmarking during development or teaching.
Example Scenario
Suppose cases.txt contains a list of pangrams (sentences using every letter of the alphabet), and some_script.py is a Python script that processes these inputs (e.g., checks if they are pangrams). The script:
- Runs
python3 some_script.pywith inputs fromcases.txt. - Measures how long it takes using
time. - Compares the script’s output to
pangrams.txtto ensure correctness. - Outputs the
timestatistics (e.g.,real 0m0.123s,user 0m0.100s,sys 0m0.020s) alongside anydiffresults.
If you modify some_script.py (e.g., optimize the algorithm), you can re-run ./test.sh python3 some_script.py to compare the new timing results, effectively profiling the impact of your changes.
Limitations
- Coarse-Grained Profiling: The
timecommand provides only high-level metrics, not detailed insights into function calls or resource usage. - Single Run: The script runs the command once per invocation. For more accurate profiling, you’d need to run it multiple times and average the results (e.g., using a loop or external tools like
hyperfine). - Output Handling: The
timeoutput is included in thediff, which might cause issues ifpangrams.txtdoesn’t account for it. You may need to filter out timing stats for clean output comparison. - Input Dependency: The script assumes
cases.txtandpangrams.txtexist and are correctly formatted.
Improvements for Better Profiling
To enhance its profiling capabilities, you could:
-
Filter
timeOutput: Redirecttime’s stderr (where timing stats are printed) to a separate file or display it without affectingdiff.diff <(cat cases.txt | eval "$@" 2>/dev/null) pangrams.txt; time "$@" -
Multiple Runs: Wrap the command in a loop to average timings over multiple executions.
-
Use
hyperfine: Replacetimewith a tool likehyperfinefor more robust benchmarking with statistical analysis. -
Verbose Output: Add logging to display timing results explicitly, even if
diffsucceeds.
Conclusion
The script is a lightweight, Unix-style tool for running a command with test inputs, measuring its execution time, and verifying its output. It acts as a basic profiler by leveraging the time command to provide performance metrics and diff to ensure correctness. Its simplicity, combined with Unix’s powerful tooling, makes it effective for quick speed testing in a classroom or development context, particularly for comparing the performance of different scripts or algorithms in a Unix environment.
diff <( cat cases.txt| time python find_pangrams.py ) pangrams.txt python find_pangrams.py 0.07s user 0.02s system 100% cpu 0.094 total
./test.sh python3 find_pangrams.py
real 0m0.090s user 0m0.073s sys 0m0.016s
- the script is making a difference even it is a same command
I’ll explain the provided C code step-by-step, assuming you have no prior experience with C. The code is a program that reads lines from standard input (e.g., the terminal or a piped file) and checks if each line is a pangram (a sentence containing every letter of the alphabet). If a line is a pangram, it prints the line. Let’s break it down clearly and concisely, introducing C concepts as we go.
Overview of the Program
- Purpose: The program reads input lines, checks if each is a pangram using the
ispangramfunction, and prints the line if it is a pangram. It also handles errors and cleans up memory. - Key Components:
- A function
ispangram(incomplete) to check if a string is a pangram. - A
mainfunction that reads input lines and processes them.
- A function
- Input/Output:
- Input: Lines from standard input (e.g., typed in the terminal or piped from a file like
cases.txt). - Output: Prints pangram lines to standard output and an “ok” message to standard error when done.
- Input: Lines from standard input (e.g., typed in the terminal or piped from a file like
Code Breakdown
1. Header Files
#include <stdbool.h>
#include <stdio.h>
#include <stdlib.h>- What are headers? In C,
#includeimports libraries (collections of functions and types) that your program needs. - Details:
<stdbool.h>: Provides thebooltype (trueorfalse). Without this, C doesn’t have a built-in boolean type (it uses integers:0for false, non-zero for true).<stdio.h>: Provides input/output functions likeprintf(print to console) andgetline(read input).<stdlib.h>: Provides memory management functions likemallocandfree, and other utilities likeexit.
2. The ispangram Function
bool ispangram(char *s) {
// TODO implement this!
return false;
}-
What it does: This function is supposed to check if a string
sis a pangram but is incomplete (it always returnsfalse). -
Key Concepts:
- Function Declaration:
bool: The return type, meaning the function returnstrueorfalse.ispangram: The function name.char *s: The parameter, a pointer to a string. In C, strings are arrays of characters (char), andchar *points to the first character.
- Strings in C: A string is an array of characters ending with a null character (
\0). For example, the string"hello"is stored as['h', 'e', 'l', 'l', 'o', '\0']. - Placeholder Implementation: The
return falseis a stub, meaning the function isn’t implemented yet. A real implementation would check ifscontains all 26 letters (ignoring case, spaces, and punctuation).
- Function Declaration:
-
What a real
ispangrammight do:- Convert the string to lowercase.
- Track which letters (a–z) appear using a boolean array or bitmask.
- Ignore non-letter characters (spaces, numbers, punctuation).
- Return
trueif all 26 letters are present,falseotherwise.
3. The main Function
int main() {- What is
main?: Themainfunction is the entry point of a C program. When you run the program, execution starts here. - Return Type:
intmeansmainreturns an integer to the operating system (usually0for success, non-zero for errors). This code doesn’t explicitly return a value, which is okay in modern C (it assumesreturn 0).
size_t len;
ssize_t read;
char *line = NULL;- Variable Declarations:
size_t len:size_tis an unsigned integer type (e.g.,unsigned long) used for sizes (like string lengths). Here, it’s initialized to an undefined value (we’ll use it withgetline).ssize_t read:ssize_tis a signed integer type (e.g.,long) used for sizes or error codes. It stores the number of characters read bygetline.char *line = NULL:lineis a pointer to a string (initially set toNULL, meaning it points to nothing). It will hold each input line.
- Why
NULL?: In C, pointers must be initialized to avoid pointing to random memory.NULLindicates the pointer isn’t yet assigned.
while ((read = getline(&line, &len, stdin)) != -1) {-
Reading Input with
getline:getline(&line, &len, stdin): A function from<stdio.h>that reads a line fromstdin(standard input, e.g., keyboard or piped file).&line: Passes the address of thelinepointer.getlinemay allocate or reallocate memory forlineto store the input.&len: Passes the address oflen.getlinesetslento the size of the allocated buffer.stdin: A file stream representing standard input.
- Return Value:
getlinereturns the number of characters read (including the newline\n) or-1if it reaches the end of input (EOF) or an error occurs. - Assignment in Loop:
read = getline(...)stores the return value inread. - Loop Condition: The
whileloop continues as long asread != -1(i.e., there’s more input to read).
-
How
getlineWorks:- If
lineisNULLor the buffer is too small,getlineallocates or resizes memory forline. - It reads characters until it hits a newline (
\n) or EOF, storing the line inline(including the\n). - It updates
lento reflect the buffer size and returns the number of characters read.
- If
if (ispangram(line))
printf("%s", line);- Processing Each Line:
ispangram(line): Calls theispangramfunction with the current line. Sinceispangramis incomplete, it always returnsfalse, so nothing is printed yet.printf("%s", line): Ifispangramreturnstrue, this prints the line to standard output (stdout). The%sformat specifier is for strings.- Note: The line includes the trailing
\n(fromgetline), soprintfpreserves it, ensuring each pangram is printed on a new line.
if (ferror(stdin))
fprintf(stderr, "Error reading from stdin");- Error Checking:
ferror(stdin): Checks if an error occurred while reading fromstdin(e.g., a file read error).fprintf(stderr, ...): Prints an error message to standard error (stderr), a separate output stream for errors (distinct fromstdout).- Why
stderr?: Errors are sent tostderrso they can be separated from normal output (e.g., when redirecting output to a file).
free(line);- Memory Cleanup:
free(line): Deallocates the memory allocated bygetlineforline. In C, you must manually free dynamically allocated memory to avoid memory leaks.- Why needed?:
getlineallocates memory forline(ifNULLor too small). Failing to free it would leak memory.
fprintf(stderr, "ok\n");- Final Message: Prints “ok” (with a newline) to
stderrto indicate the program completed. - Why
stderr?: Likely to separate status messages from the actual output (pangrams), which go tostdout.
How It Fits with the Bash Script
From your previous question, the Bash script (test.sh) runs this program with input from cases.txt and compares its output to pangrams.txt. Here’s how they connect:
- Input: The Bash script pipes
cases.txt(e.g., a list of test strings) to the C program’sstdin. - Processing: The C program reads each line, checks if it’s a pangram (once
ispangramis implemented), and prints pangram lines tostdout. - Output Comparison: The Bash script uses
diffto compare the C program’s output (pangram lines) topangrams.txtto verify correctness. - Timing: The Bash script’s
timecommand measures how long the C program takes, useful for profiling.
For example, if cases.txt contains:
The quick brown fox jumps over the lazy dog
Hello world
A pangram is fun
And pangrams.txt contains only the pangram:
The quick brown fox jumps over the lazy dog
The C program (with a working ispangram) would print only the first line, and diff would check if it matches pangrams.txt.
Key C Concepts for Beginners
Here’s a quick primer on C concepts in this code, since you’re new to C:
-
Pointers (
*):- A pointer is a variable that stores a memory address.
char *linepoints to a string’s first character. &variablegets the address of a variable, used to modifylineandleningetline.
- A pointer is a variable that stores a memory address.
-
Memory Management:
- C doesn’t have automatic garbage collection. You allocate memory (e.g.,
getlinedoes this) and must free it withfree. - Failing to
freecauses memory leaks.
- C doesn’t have automatic garbage collection. You allocate memory (e.g.,
-
Standard Input/Output:
stdin: Where input comes from (keyboard, file, or pipe).stdout: Where normal output goes (console or file).stderr: For error messages or status.
-
Strings:
- Strings are
chararrays ending with\0. - Functions like
printfandgetlinehandle strings viachar *.
- Strings are
-
Types:
size_t: Unsigned integer for sizes (e.g., buffer lengths).ssize_t: Signed integer for sizes or error codes (e.g.,getline’s return).bool: Boolean type (trueorfalse) from<stdbool.h>.
Example: Completing ispangram
Since ispangram is incomplete, here’s a simple implementation to make the program functional:
bool ispangram(char *s) {
bool letters[26] = {false}; // Track a-z
for (int i = 0; s[i] != '\0'; i++) {
char c = s[i];
// Convert to lowercase and check if it's a letter
if (c >= 'A' && c <= 'Z') c = c + ('a' - 'A');
if (c >= 'a' && c <= 'z') {
letters[c - 'a'] = true; // Mark letter as seen
}
}
// Check if all letters are present
for (int i = 0; i < 26; i++) {
if (!letters[i]) return false;
}
return true;
}- How it works:
- Creates a boolean array to track letters a–z.
- Iterates through the string
s. - Converts uppercase to lowercase (e.g.,
'A'to'a') and ignores non-letters. - Marks each letter’s index (e.g.,
'a'→ index 0,'b'→ index 1) astrue. - Returns
trueonly if all 26 letters were seen.
Running the Program
-
Compile: Save the code as
pangram.cand compile it withgcc:gcc -o pangram pangram.cThis creates an executable named
pangram. -
Run Manually:
./pangramType lines (e.g., “The quick brown fox jumps over the lazy dog”), and press Ctrl+D (EOF) when done. Pangrams will be printed.
-
With the Bash Script: If
cases.txtexists, run:./test.sh ./pangramThis pipes
cases.txtto the program, times it, and compares output topangrams.txt.
Sample Run
Input (cases.txt):
The quick brown fox jumps over the lazy dog
Hello world
With ispangram implemented:
- The program reads each line.
- Checks if it’s a pangram (only the first line is).
- Prints:
The quick brown fox jumps over the lazy dog - Prints to
stderr:ok
Bash Script Output:
- If
pangrams.txtmatches the output,diffshows nothing (success). timeshows execution time (e.g.,real 0m0.010s).
Why This Code?
This code is likely part of a programming assignment (as hinted by your teacher’s Bash script). It teaches:
- Reading input in C (
getline). - String processing (
ispangram). - Memory management (
free). - Error handling (
ferror). - Integration with Unix tools (via
stdin/stdout).
Next Steps
- Try Implementing
ispangram: Use the example above or experiment with your own logic. - Test It: Create a
cases.txtwith pangrams and non-pangrams, and use the Bash script to test. - Learn More C:
- Practice with pointers (
*,&). - Explore string functions in
<string.h>(e.g.,strlen,strtolower). - Read about
getlineand dynamic memory in C.
- Practice with pointers (
If you have questions about specific parts or want help with ispangram, let me know!
the different C compiler , gcc vs clang
-
Compiler Explorer can show clang and gcc result at the same time
-
The Architecture of Open Source Applications (Volume 1)LLVM AOSA book
llvm got more reusable tools
rust → write a front end llvm → easy to use and build cross different os env
Type definitions and literals in C
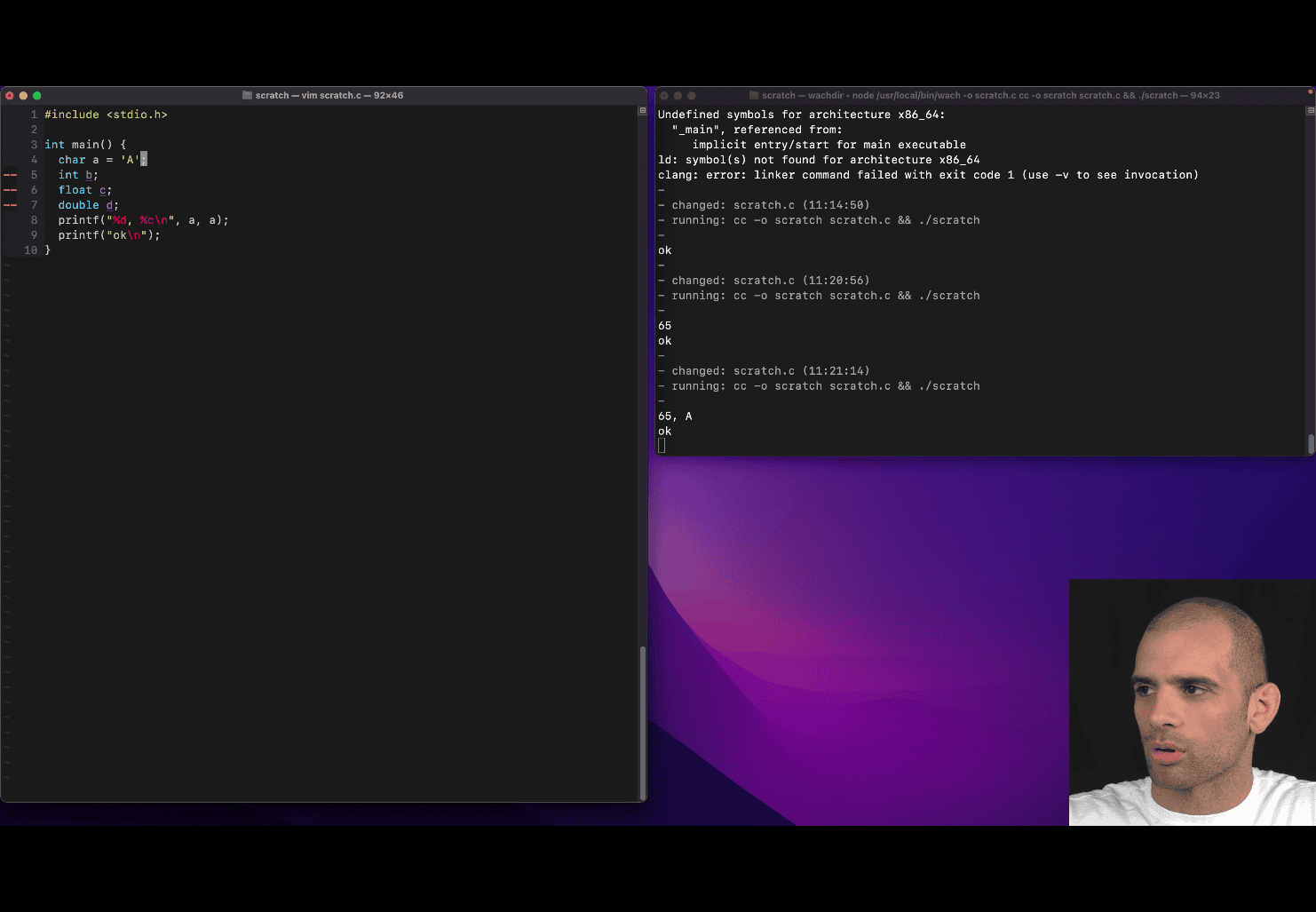
include <stdio.h> printf (“%d, %c\n”, a, a) ; → this print the same a in different format c → character
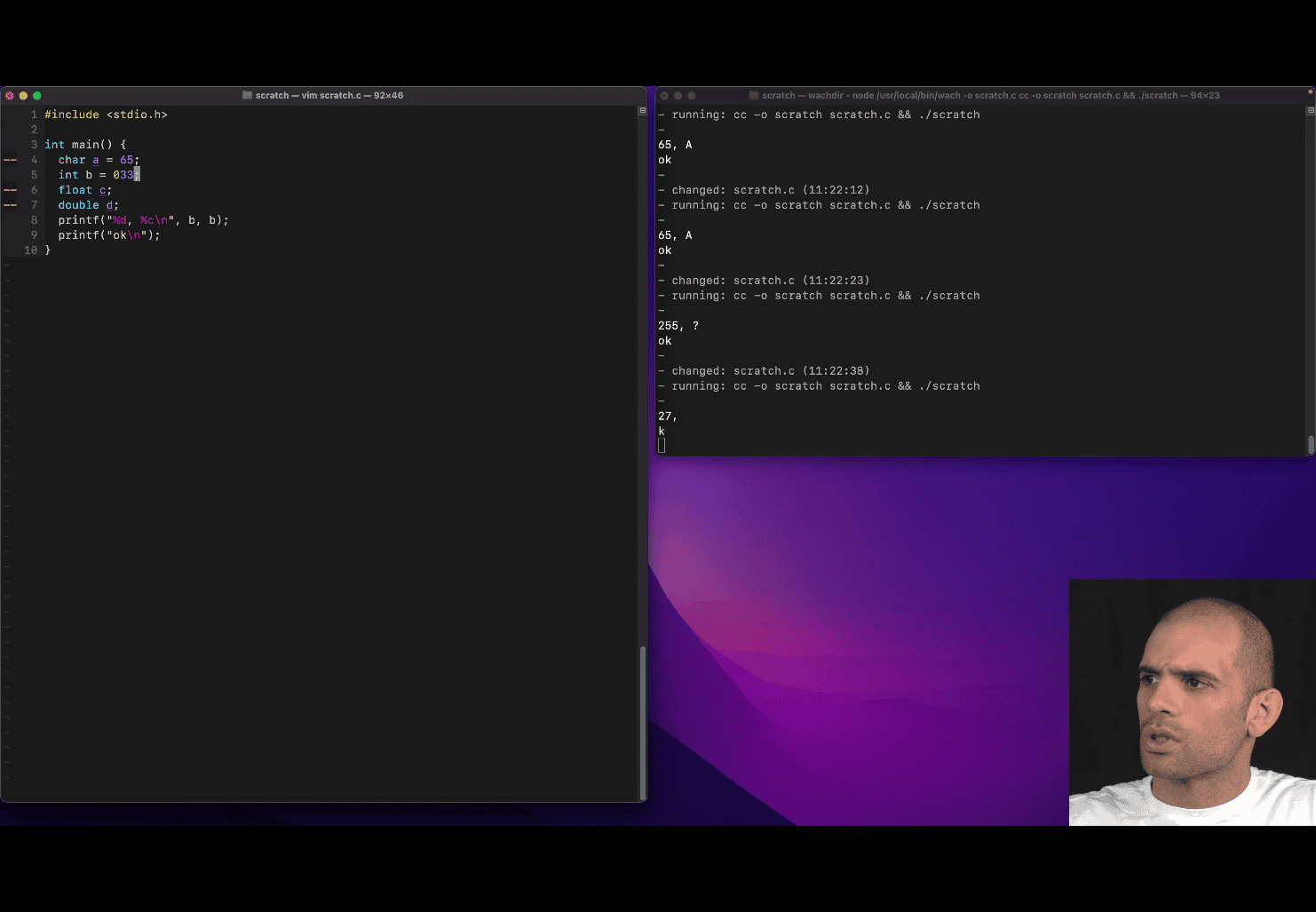 int b 033; → octal
can’t do 0b11 in c , but compiler will do that for you
int b 033; → octal
can’t do 0b11 in c , but compiler will do that for you
“%f\n”, c (float, 0.3)
long int e = 20L; (“L”→ imply this is a L (long) )
long e = 20L; (skip the “int” if using L)
short int f = 5; short f = 5; (still make sure)
long and short is mechine related
short < = to int
int < = to long
The number of bits used by a normal int type in C is not fixed by the standard but has a required minimum size and commonly used sizes depending on the platform.
- Minimum size: The C standard specifies that
intmust be at least 16 bits 2 bytes[2][5][6]. - Common actual sizes: On most modern systems,
intis typically 32 bits (4 bytes), but it can also be 16 bits on some older or embedded systems[2][3][4][5][6]. - Platform-dependent: The exact size of
intdepends on the compiler and the hardware architecture. To find the size on your specific system, you can use thesizeof(int)operator in C code[2][5].
Summary Table
| Type | Minimum bits (C standard) | Common sizes |
|---|---|---|
| int | 16 | 16 or 32 |
Key points:
intmust be at least 16 bits, but is usually 32 bits on modern computers[1][2][4][5][6].- The size is chosen to match what is most efficient for the target processor[1].
- Always check with
sizeof(int)if you need to know the exact size on your platform[2][5].
Example C code to check size:
printf("int is %zu bytes\n", sizeof(int));In summary, a normal int in C is at least 16 bits, but is most commonly 32 bits on contemporary systems
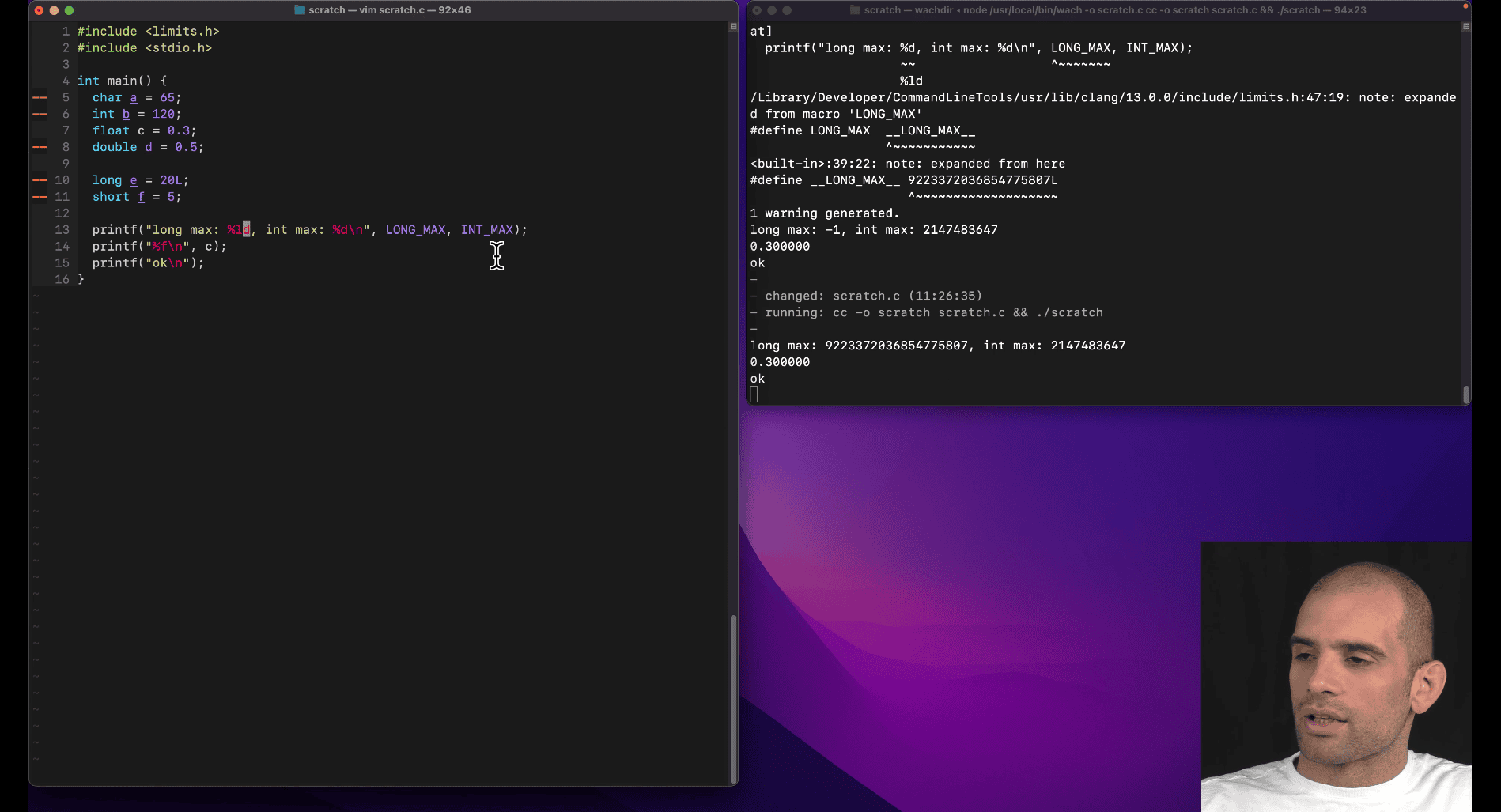 %ld → long digit, %d → max int
include <limits.h> → show the limits
%ld → long digit, %d → max int
include <limits.h> → show the limits
unsigned g ; and givin bits to variable
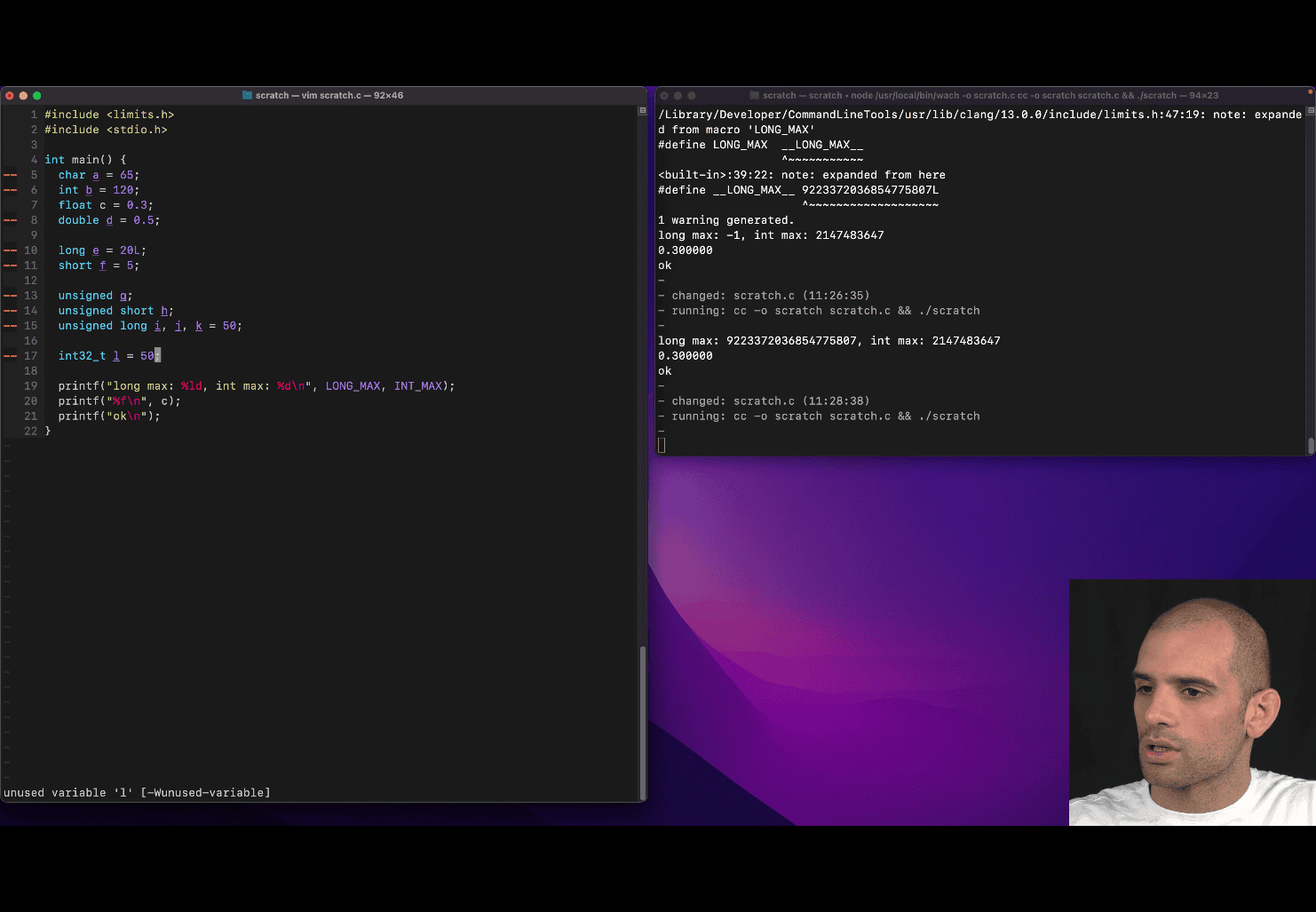
include <stdint.h>
int32_t l = 50;
Key Features of <stdint.h>
-
Fixed-Width Integer Types
Provides types like
int8_t,int16_t,int32_t,int64_t(signed) anduint8_t,uint16_t,uint32_t,uint64_t(unsigned).These types guarantee the exact number of bits, regardless of the platform.
-
Minimum and Fastest Integer Types
Defines types like
int_least8_t,int_least16_t, etc., which guarantee at least the specified width.Defines types like
int_fast8_t,int_fast16_t, etc., which are the fastest types with at least the specified width. -
Maximum Integer Types
intmax_tanduintmax_trepresent the largest signed and unsigned integer types supported by the implementation. -
Macros for Limits
Macros such as
INT32_MAX,UINT8_MAX, etc., provide the maximum and minimum values for each type.
Loop syntax in C
// int n = 5;
for (int m = 5; m > 0; m--) {
printf("%d\n", m);
}is same as
for (int m = 5; m; m--) {
same logic → all place in one place then use for loop
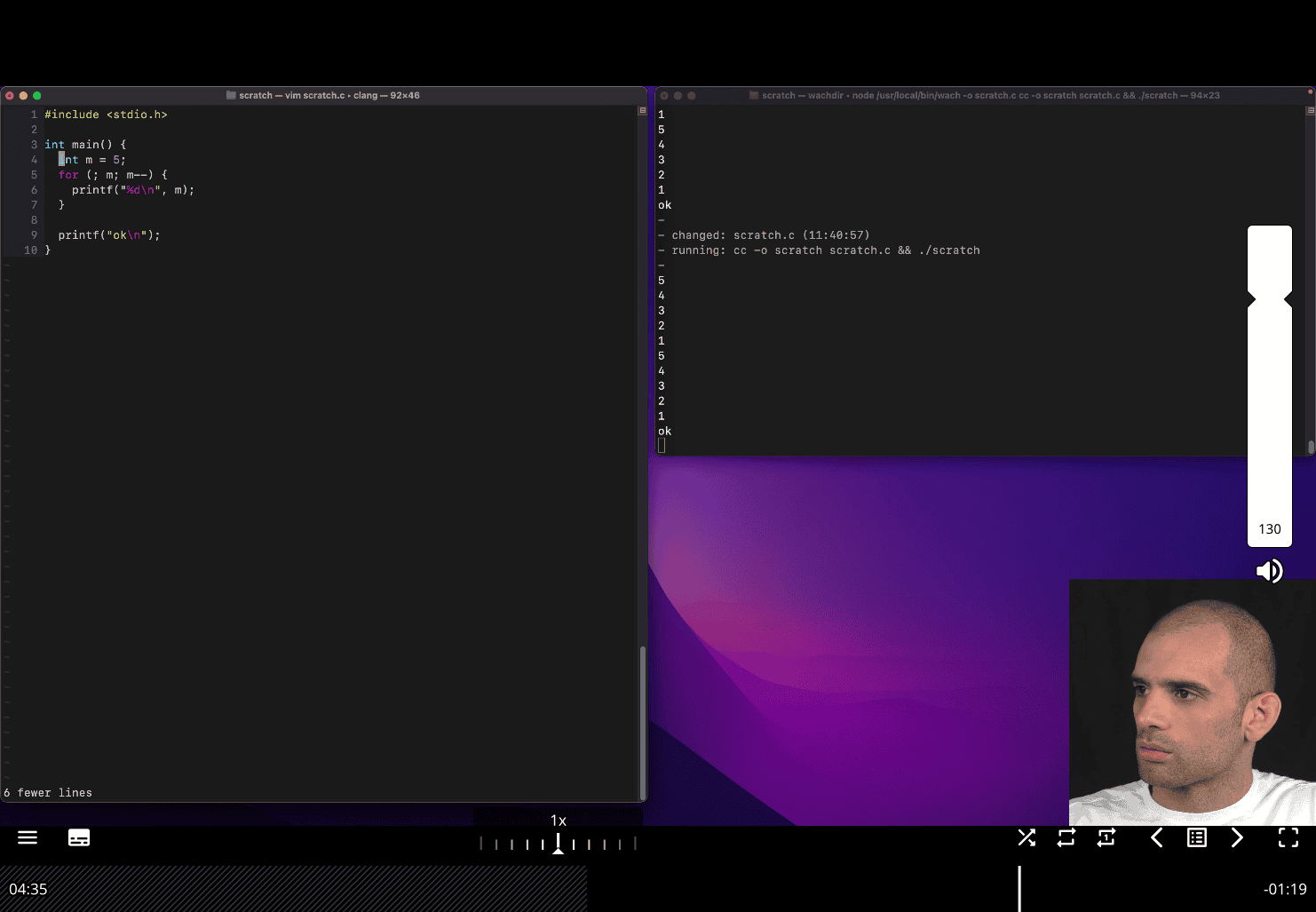
you don have to initate in the for loop statment s
for loop in while like:
for (;;){
}
for (;m;;){}
for(;;){}→while (1){}
do while (in end )
- What is the effect of the compiler optimization level flag?
- sometime you may prefer other one , for debugging and readability e.g O1 maybe
e.g in unix , you don’t want run all the optimization and just use the thing in the development
- What is a register?
cc -O1 -g -o inc inc.c using lldb ./inc
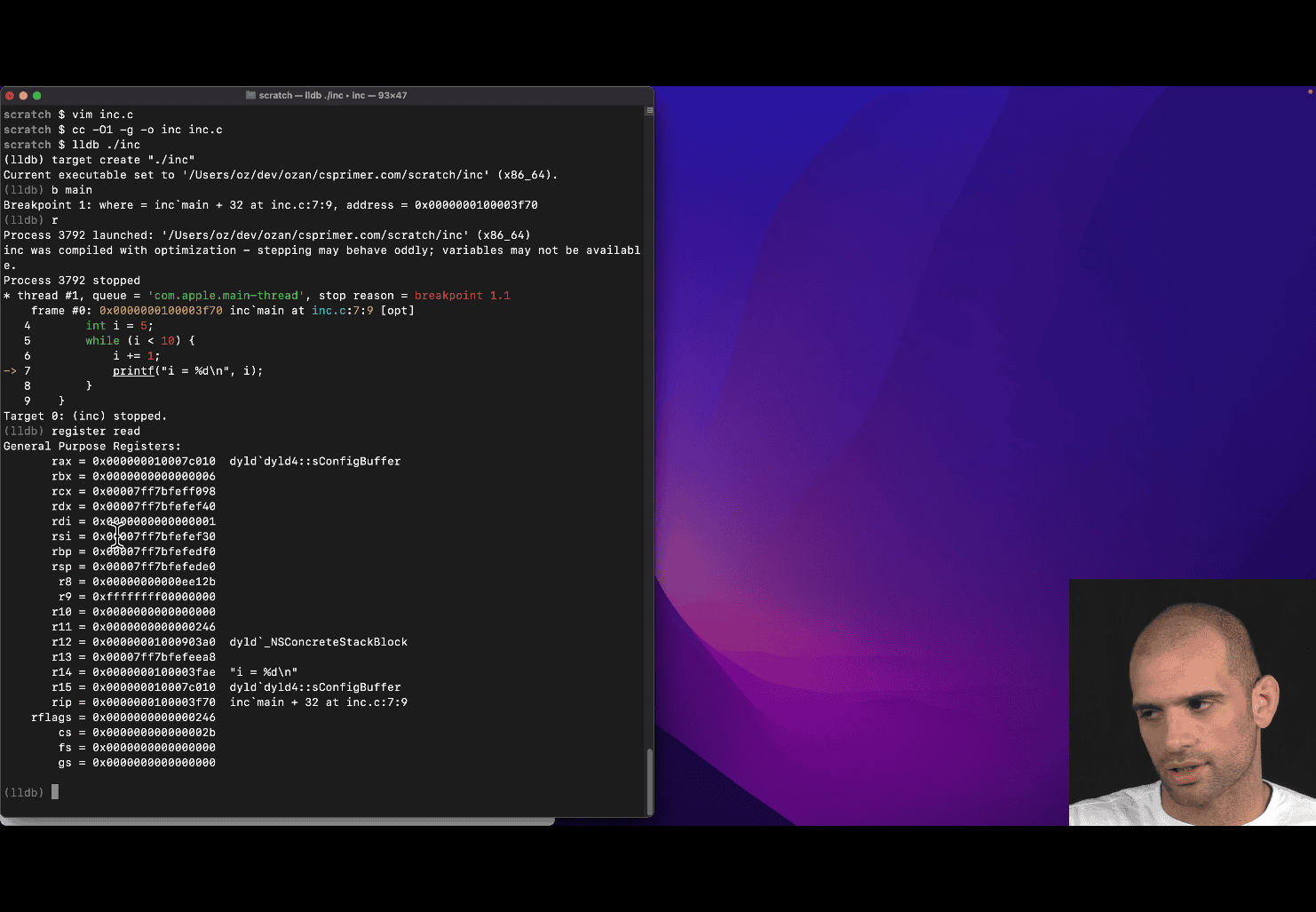
rbx → compiler chosen to store the value of “i”
reg re → short form of register read
reg re rbx
and apply format function to help reading
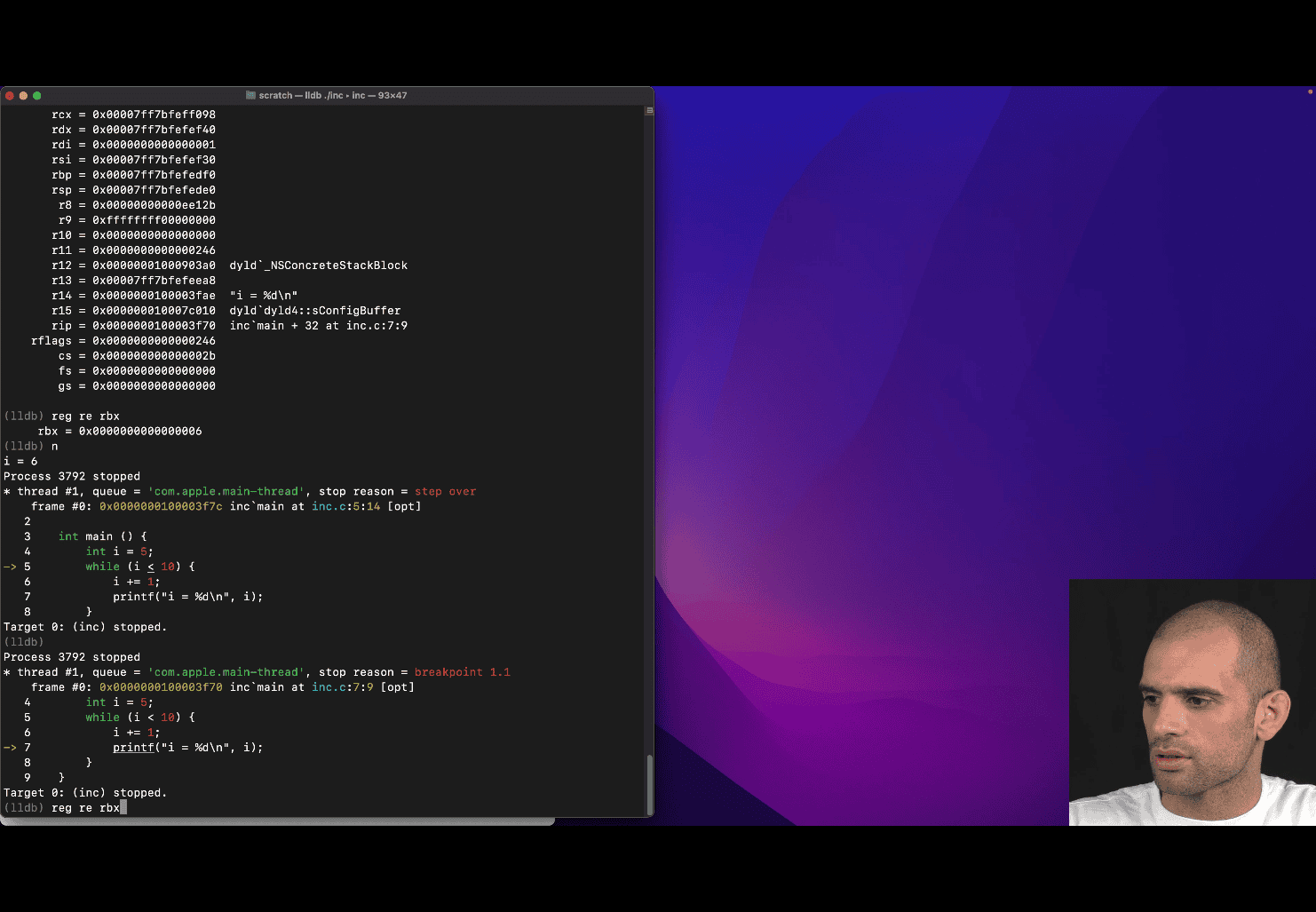
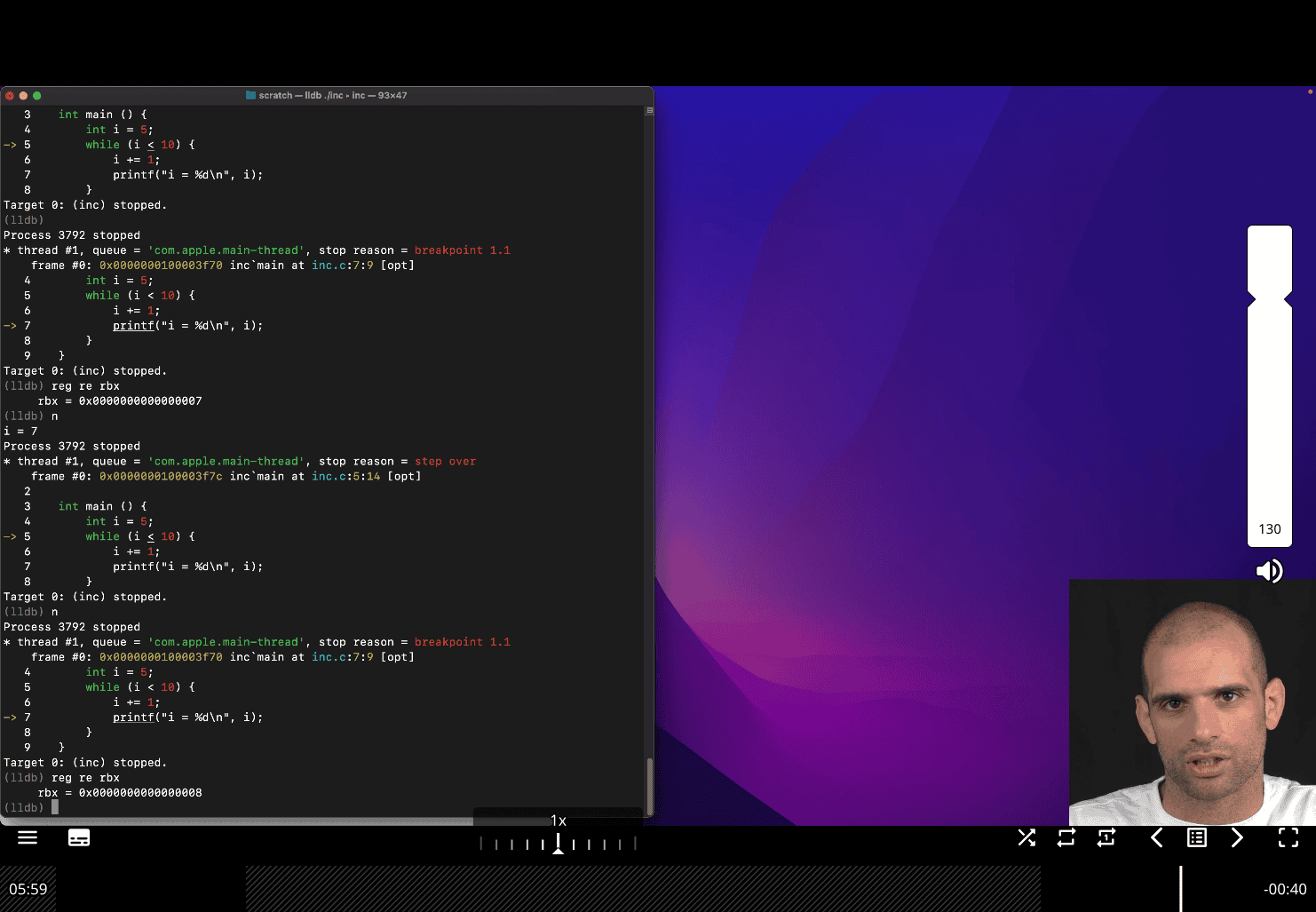
this is useful skill to check what is going on register, and register is run faster than ram
- Overview of pointers and arrays in C
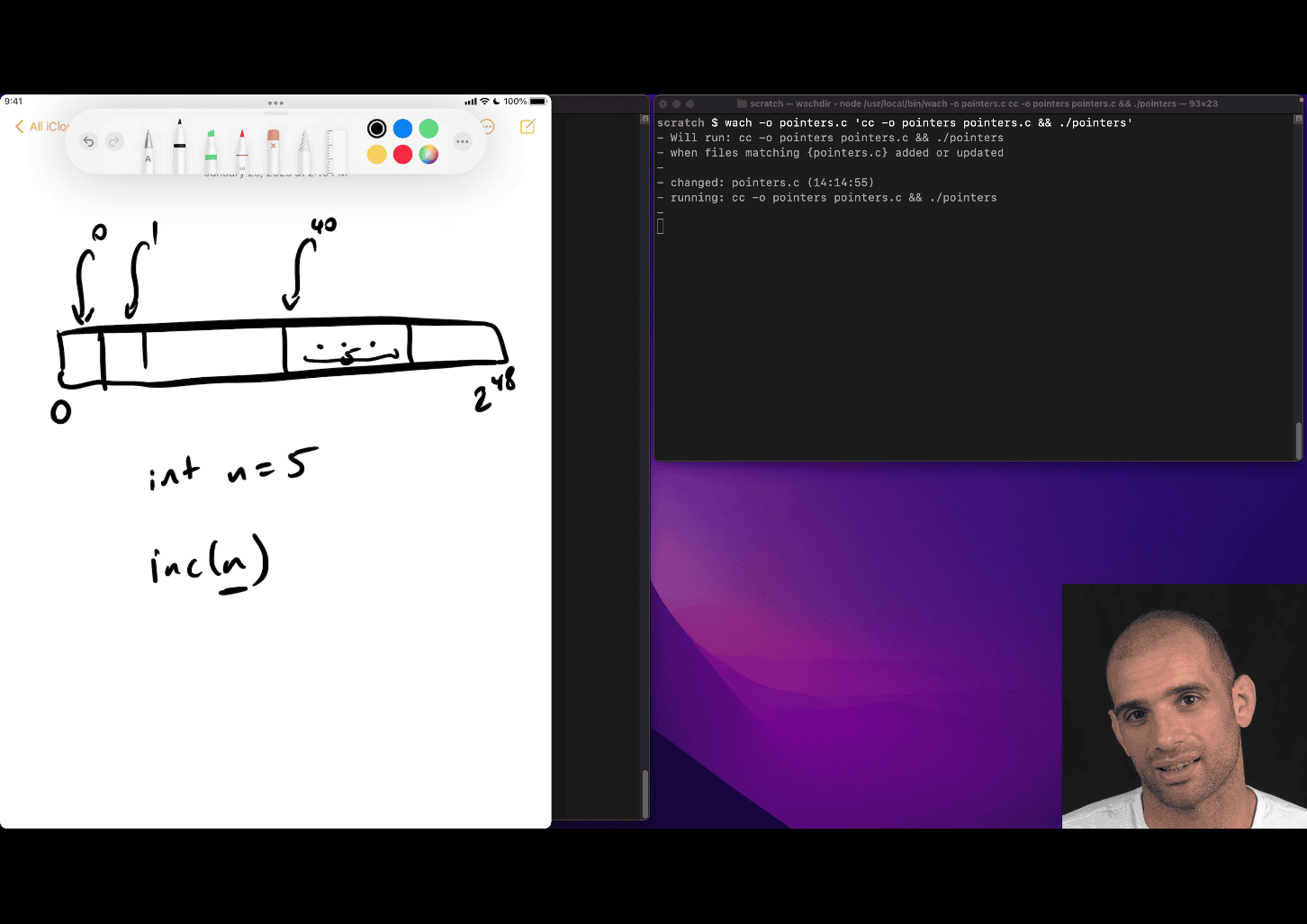
- need to pass the address to really change the value in that n = value location
inc (&n)
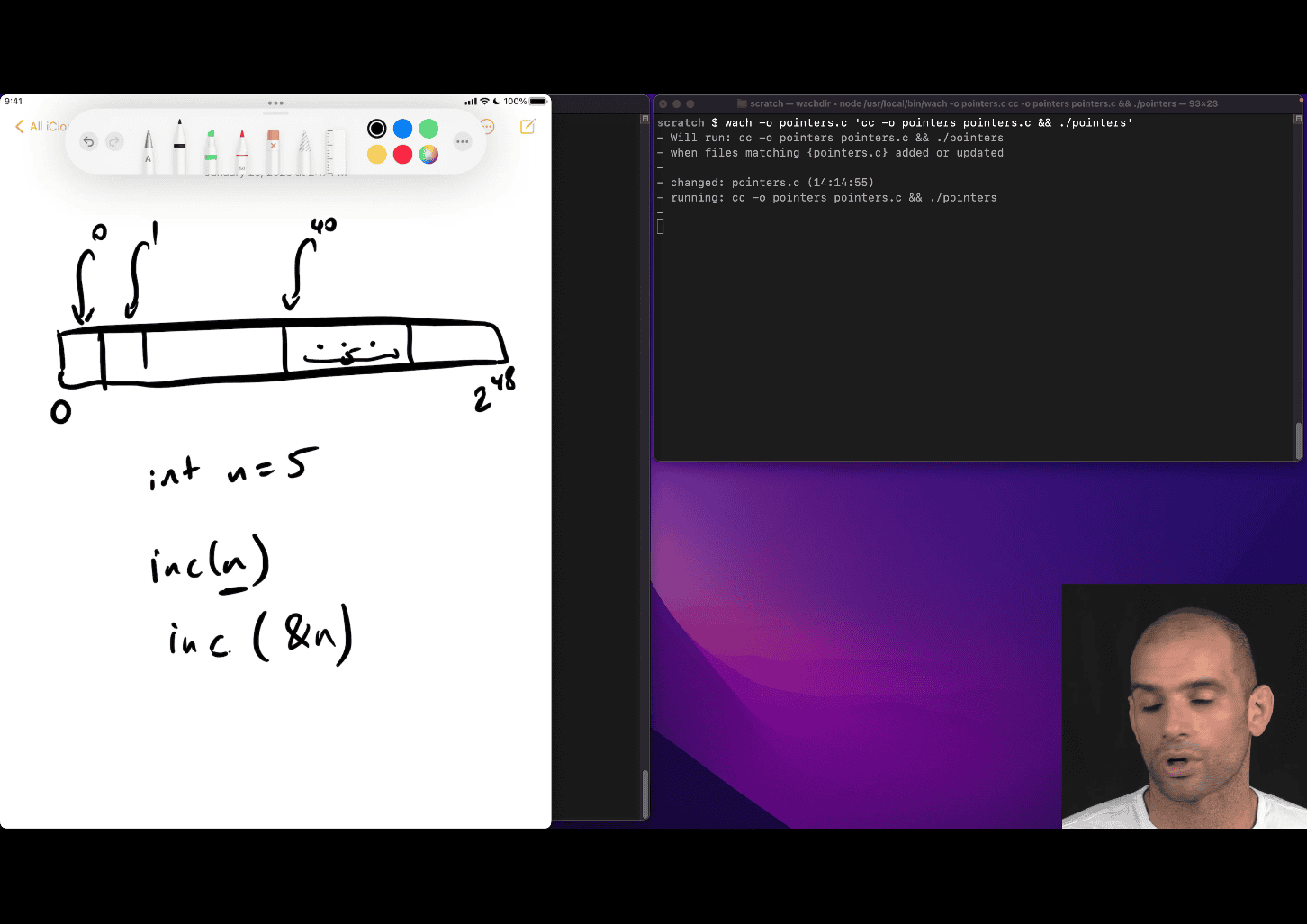 location is 40 in that cases
location is 40 in that cases
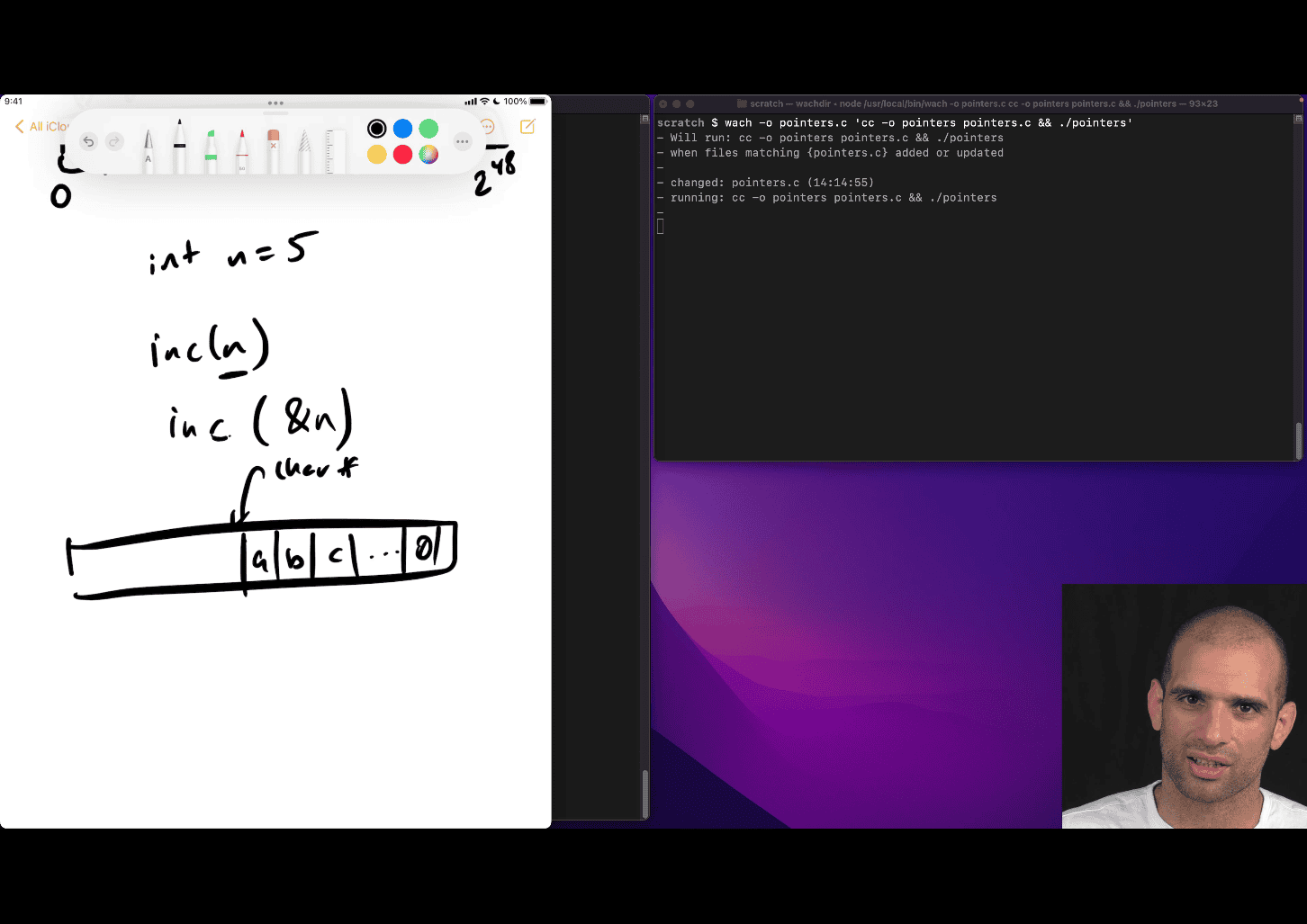
char * → inc(the address) then get a , inc one more → b
last 0 → imply it is the end
other reason, two return value e.g. need address
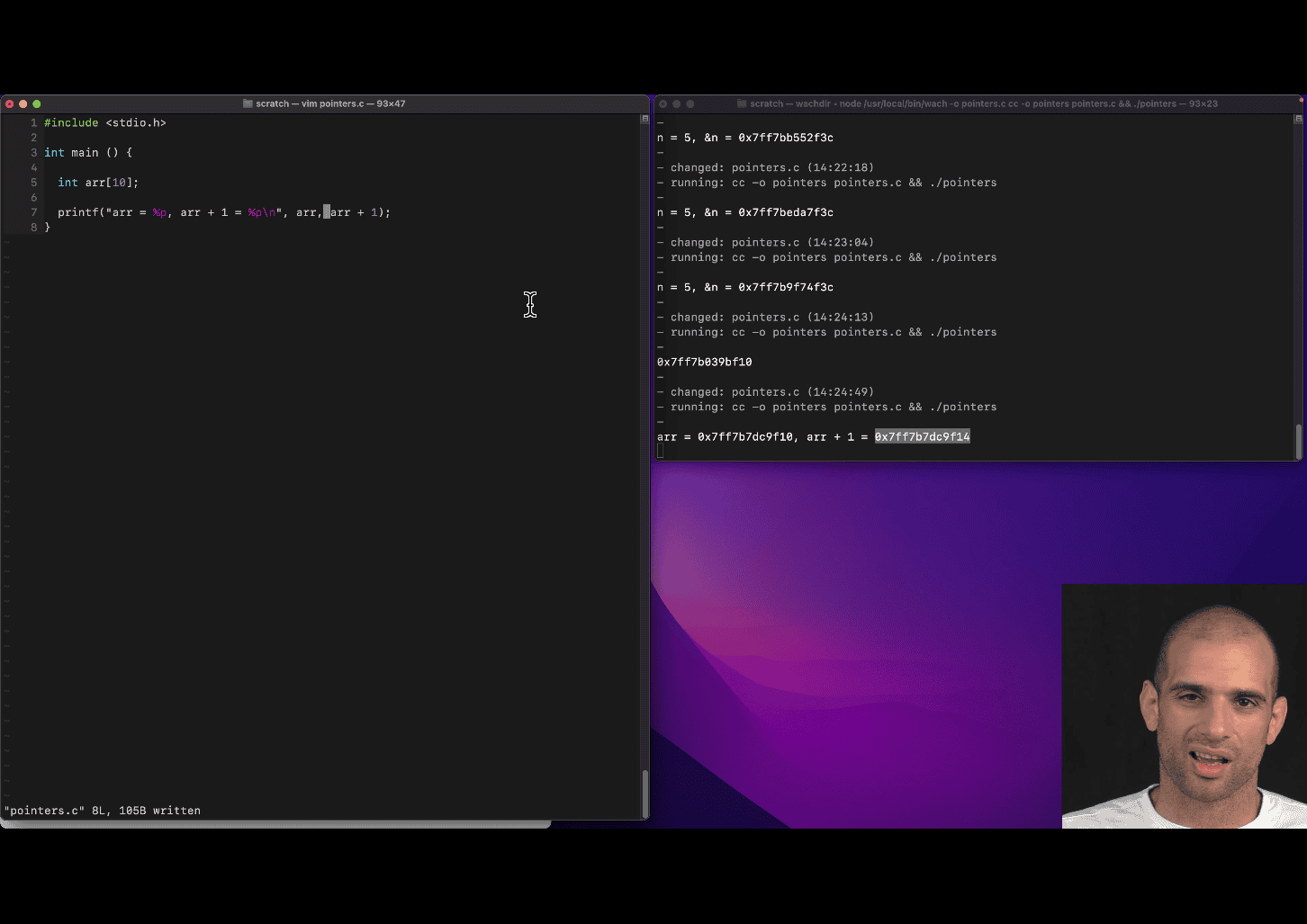
#include <stdio.h>
int main() {
int n = 5;
printf("*n = %d, &n = %p\n", n, (void*)&n);
return 0;
}#include <stdio.h>
int main() {
int n = 5;
int *p = &n;
// printf("n = %d, &n = %p\n", n, (void *)&n);
printf("n = %d, &n = %p\n", n, p);
}
-
same thing ,
*pis just reminder as int pointer, more likeint* p -
int foo = *p;→ * is a pointer , follow the pointer p → get the value→ that’s foo (Dereferencing) -
Dereferencing
array are syntax for pointer
array → starting location of a thing, need type etc
int arr[10];
printf("%p",arr) %p → pointer
take the pointer of arr[3]→ return 42
deference ⇒ *()
- deference ⇒
*()
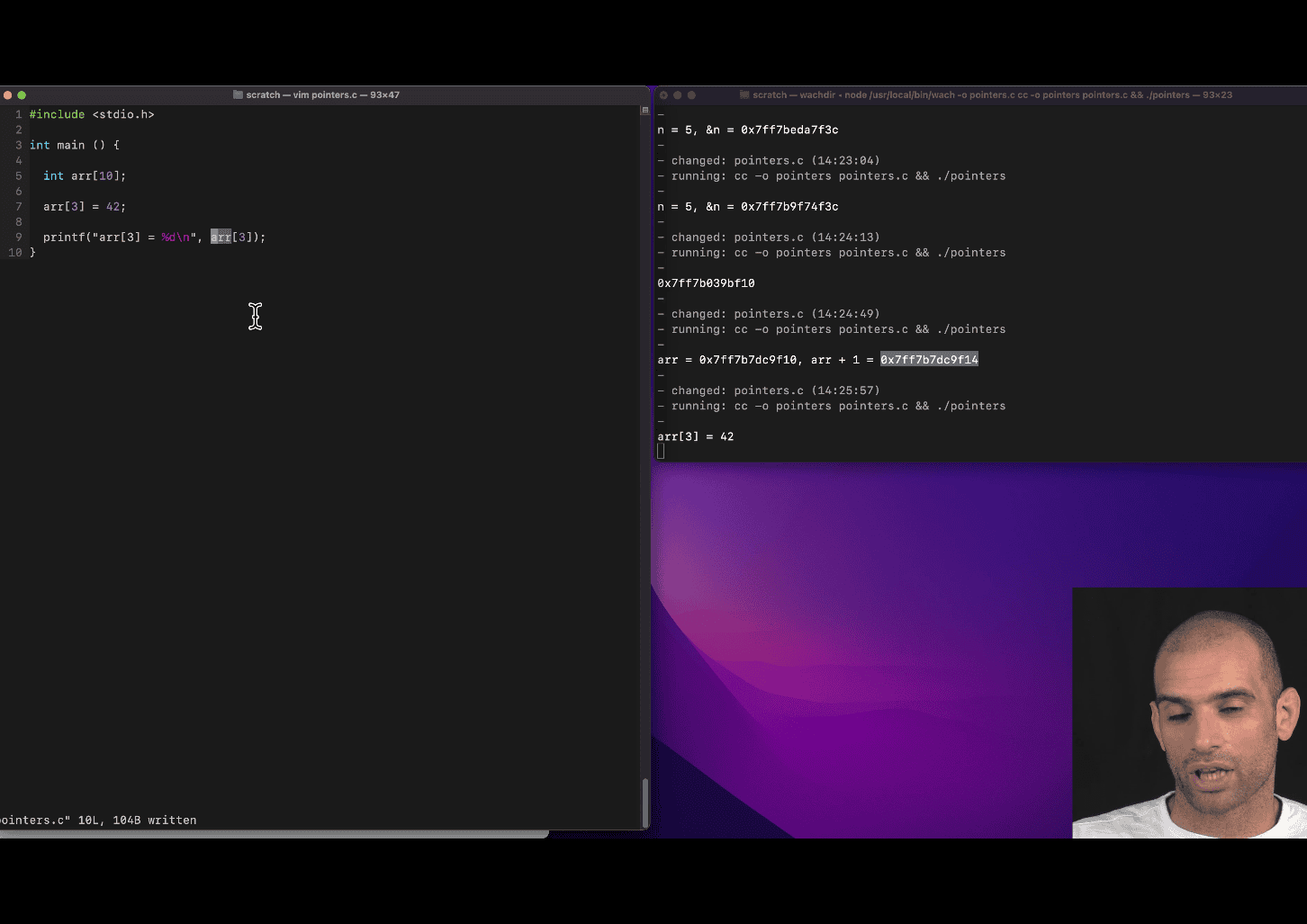
#include <stdio.h>
int main() {
int arr[16];
arr[3] = 42;
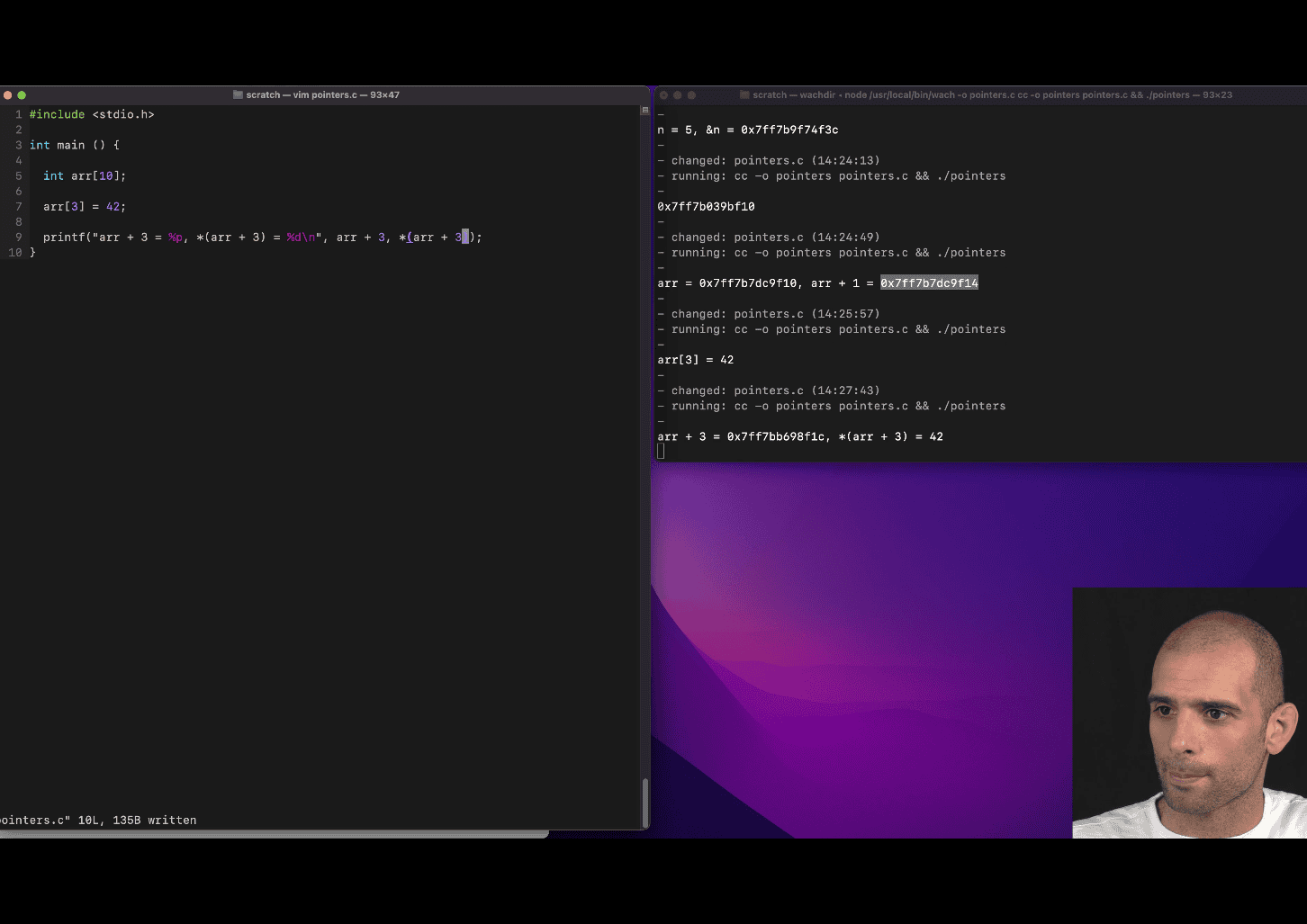
printf("*arr + 3 = %p, *(arr + 3) = %d\n", arr + 3, *(arr + 3));
return 0;
}Your teacher is introducing you to the concept of pointers in C and how array indexing relates to pointer arithmetic. Let’s break down the key idea behind arr[3] being equivalent to *(arr + 3).
1. Arrays and Pointers in C
In C, an array (like int arr[16]) is closely related to pointers. When you declare an array, the name arr represents the base address of the array, which is the memory address of the first element (arr[0]). This means arr is effectively a pointer to the starting point of the array in memory.
Each element in the array is stored in contiguous memory locations, and the size of each element depends on the data type (e.g., int is typically 4 bytes on most systems).
2. Array Indexing: arr[3]
When you write arr[3], you’re accessing the element at index 3 of the array. This is a convenient syntax for accessing elements, but under the hood, C uses pointer arithmetic to locate the memory address of arr[3].
3. Pointer Arithmetic: *(arr + 3)
The expression *(arr + 3) is the pointer-based equivalent of arr[3]. Let’s break it down:
arris the base address of the array (a pointer toarr[0]).arr + 3performs pointer arithmetic. It calculates the memory address of the element that is 3 positions beyond the base address. Since eachinttakes up a fixed number of bytes (e.g., 4 bytes),arr + 3points to the address ofarr[3].- The
*operator dereferences the pointer, meaning it retrieves the value stored at the addressarr + 3. So,*(arr + 3)gives you the value ofarr[3].
4. Why arr[3] == *(arr + 3)?
In C, the array indexing syntax arr[i] is syntactic sugar for *(arr + i). This means:
arr[3]is exactly the same as*(arr + 3).- Both expressions compute the address of the element at index 3 and retrieve its value.
This equivalence exists because arrays are implemented as pointers in C, and the indexing operation is just a shorthand for pointer arithmetic and dereferencing.
5. Example from Your Code
In your code:
int arr[16];
arr[3] = 42;
printf("*arr + 3 = %p, *(arr + 3) = %d\n", arr + 3, *(arr + 3));arr + 3computes the memory address ofarr[3]. The%pformat specifier prints this address (e.g., some hexadecimal value like0x7ffee4a0c0c).*(arr + 3)dereferences that address to get the value stored there, which is42(since you setarr[3] = 42). The%dformat specifier prints this value.
6. What Your Teacher Is Teaching
Your teacher is emphasizing that:
- Arrays and pointers are deeply connected in C.
- Array indexing (
arr[i]) is just a convenient way to perform pointer arithmetic (*(arr + i)). - Understanding pointer arithmetic is key to mastering pointers, as it shows how C navigates memory to access array elements.
- By using
*(arr + 3), you’re directly manipulating memory addresses, which is what C is doing behind the scenes when you writearr[3].
7. Key Takeaways
arr[3]and*(arr + 3)are equivalent ways to access the same element.arr + 3gives you the address ofarr[3].*(arr + 3)dereferences that address to get the value (e.g.,42).- This concept is fundamental to understanding pointers, memory management, and how arrays work in C.
8. A Visual Explanation
Imagine the array arr in memory (assuming int is 4 bytes):
Index: arr[0] arr[1] arr[2] arr[3] ...
Address: 1000 1004 1008 1012 ...
Value: ? ? ? 42 ...
arrpoints to address1000(base address).arr + 3points to address1012(base + 3 * sizeof(int)).*(arr + 3)retrieves the value at address1012, which is42.arr[3]does the same thing but with simpler syntax.
9. Practice to Reinforce
To solidify this, try experimenting with your code:
- Print
arr[3]and*(arr + 3)to confirm they’re identical. - Print the addresses
&arr[3]and(arr + 3)to see they point to the same location. - Try accessing other indices (e.g.,
arr[5]vs.*(arr + 5)) to build intuition.
#include <stdio.h>
int main() {
int arr[16];
arr[3] = 42;
arr[5] = 99;
printf("arr[3] = %d\n", arr[3]);
printf("*(arr + 3) = %d\n", *(arr + 3));
printf("pointer of arr3 = %p\n", &arr);
printf("&arr[3] = %p\n", (void *)&arr[3]);
printf("arr + 3 = %p\n", (void *)(arr + 3));
printf("arr[5] = %d\n", arr[5]);
printf("*(arr + 5) = %d\n", *(arr + 5));
printf("pointer of arr5 = %p\n", &arr);
printf("&arr[5] = %p\n", (void *)&arr[5]);
printf("arr + 5 = %p\n", (void *)(arr + 5));
return 0;
// > gcc -O1 -g -o demo demo.c && ./demo
// arr[3] = 42
// *(arr + 3) = 42
// pointer of arr3 = 0x7ffd0753f1d0
// &arr[3] = 0x7ffd0753f1dc
// arr + 3 = 0x7ffd0753f1dc
// arr[5] = 99
// *(arr + 5) = 99
// pointer of arr5 = 0x7ffd0753f1d0
// &arr[5] = 0x7ffd0753f1e4
// arr + 5 = 0x7ffd0753f1e4
}
arr points to address 1000 (base address). arr + 3 points to address 1012 (base + 3 _sizeof(int)). _(arr + 3) retrieves the value at address 1012, which is 42. arr[3] does the same thing but with simpler syntax.
- The C pre-processor, macros and conditional inclusion
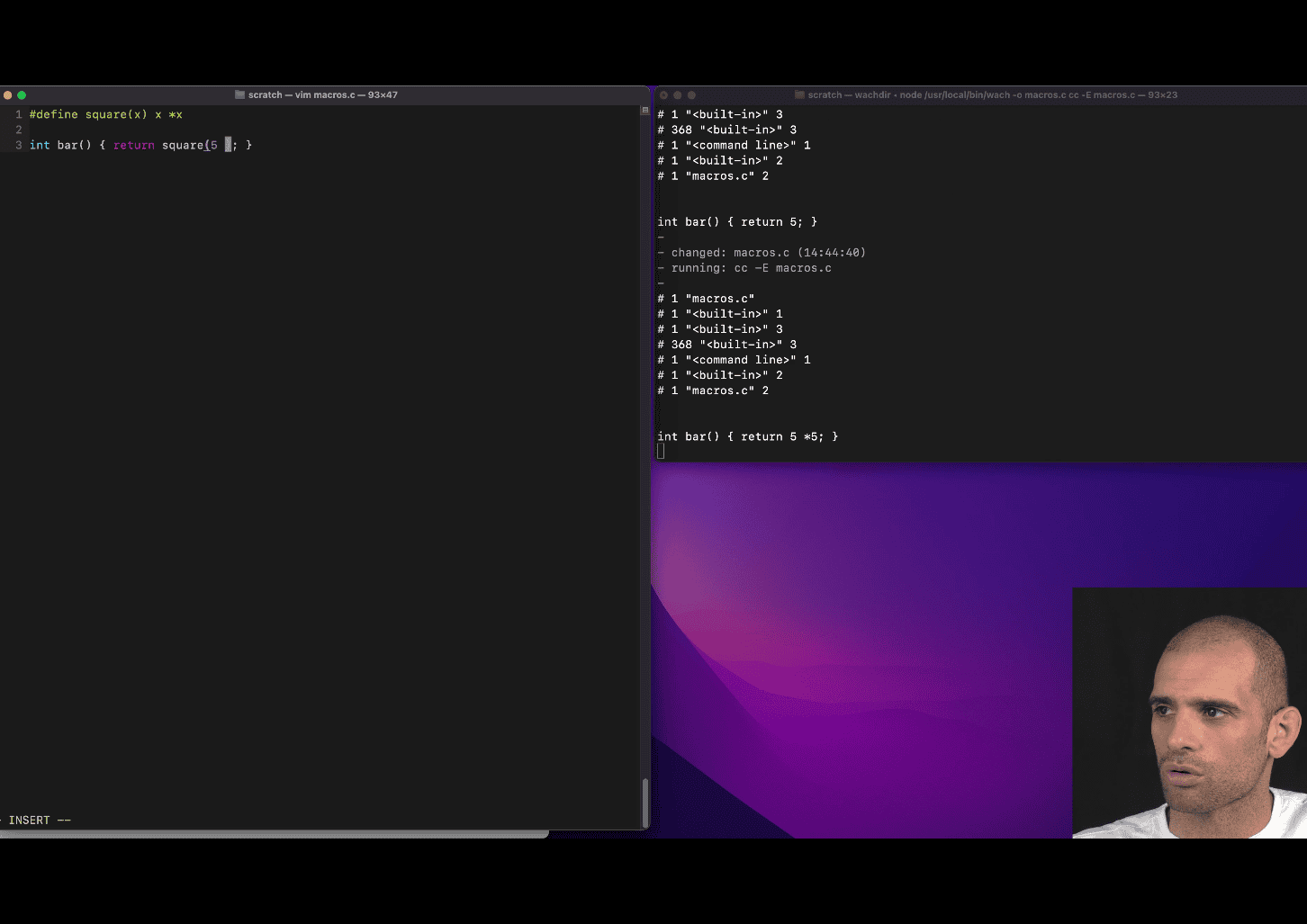
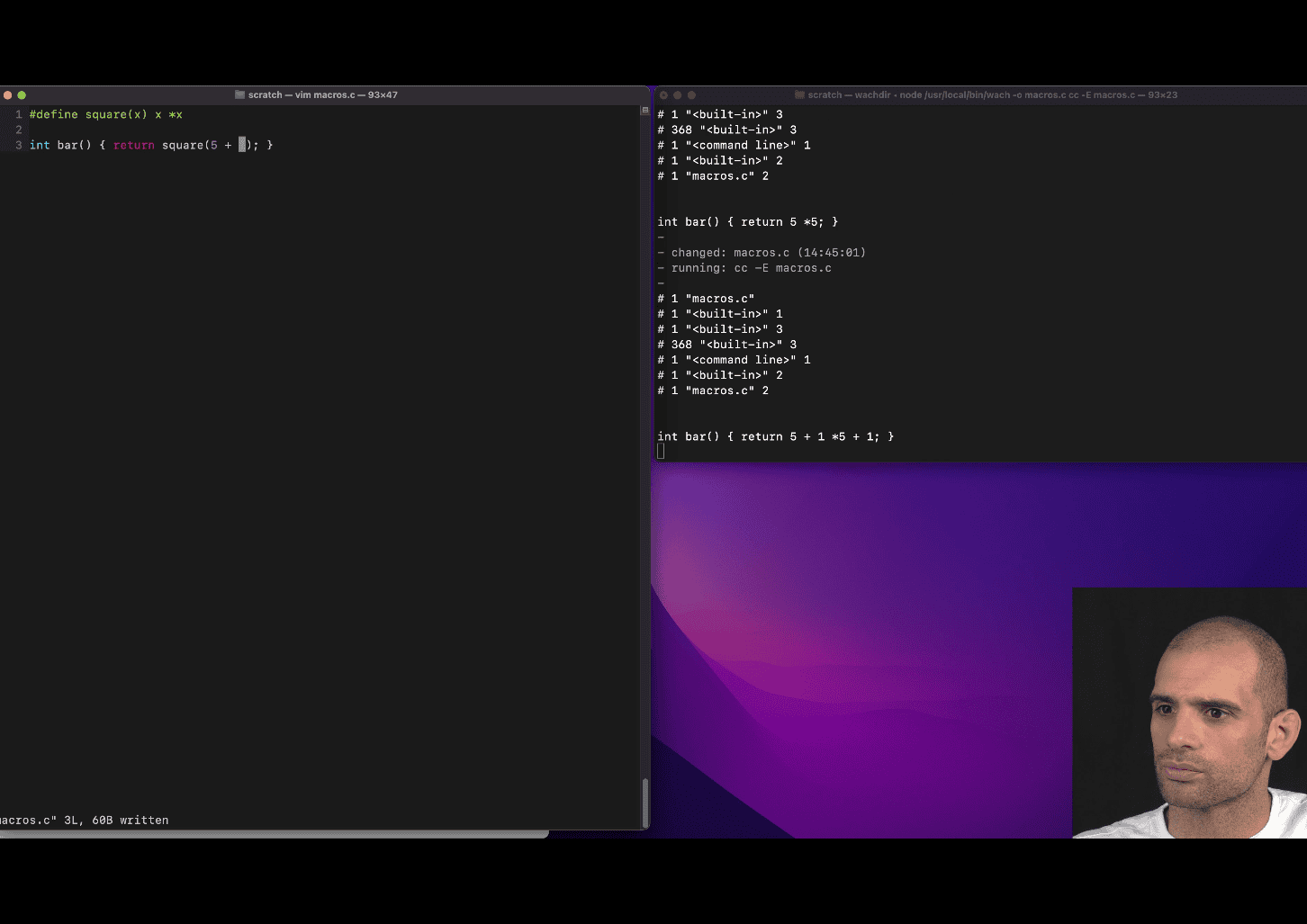
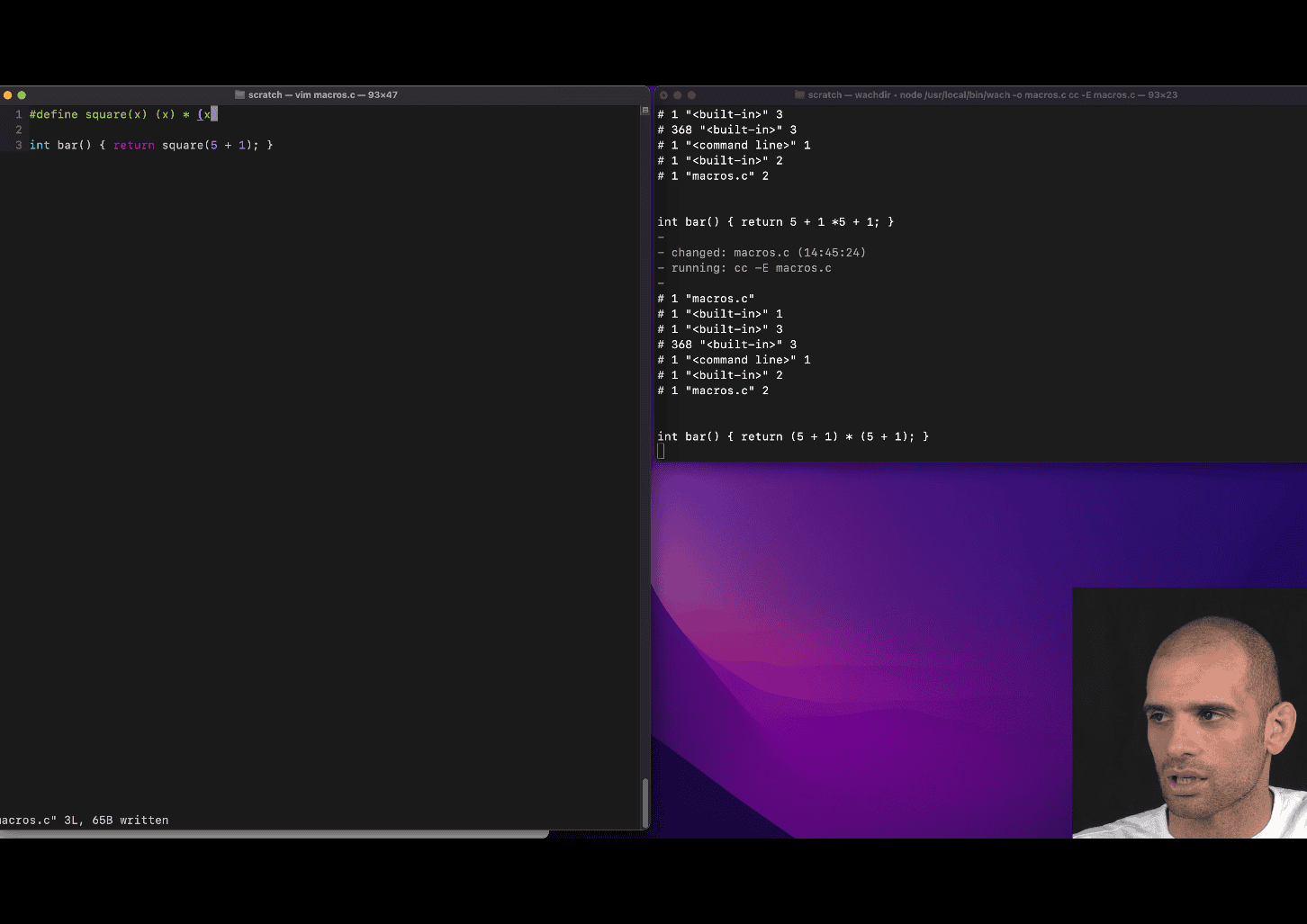
#define square(x) (x)*(x)
text replacement feature before compiler
include is also is part of this
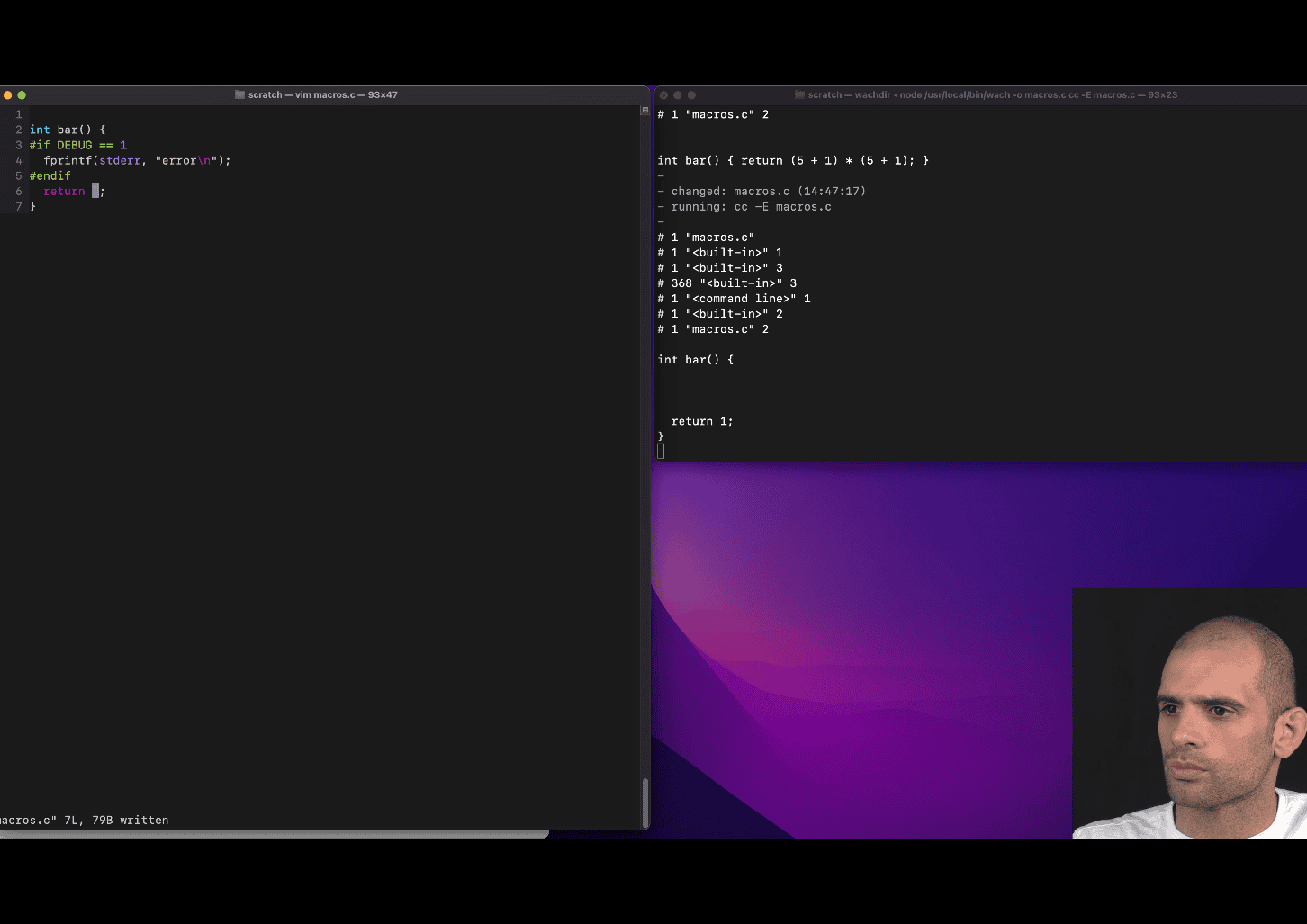
Your teacher is introducing you to conditional compilation in C using preprocessor directives like #if, #endif, and likely the concept of macros (e.g., DEBUG). The code snippet you provided has a few issues (e.g., syntax errors), but I’ll interpret it as a teaching example and explain the key concepts based on the corrected version:
int bar() {
#if DEBUG == 1
fprintf(stderr, "error\n");
#endif
return 1;
}Let’s break down what your teacher is trying to teach you.
1. Preprocessor Directives
The C preprocessor is a tool that processes your code before it is compiled. It handles directives starting with #, such as #if, #endif, #define, etc. In this example:
#if DEBUG == 1checks whether the macroDEBUGis defined and has the value1.#endifmarks the end of the conditional block.- The code inside the
#ifblock (i.e.,fprintf(stderr, "error\n");) is only included in the compiled program if the conditionDEBUG == 1is true.
2. Conditional Compilation
Conditional compilation allows you to include or exclude parts of your code based on certain conditions. This is useful for:
- Debugging: Including debug-specific code (like error messages) only when a debug mode is enabled.
- Portability: Including different code for different platforms or configurations.
- Feature toggling: Enabling or disabling features without changing the source code.
In this case:
- If
DEBUGis defined as1(e.g., via a#define DEBUG 1or a compiler flag like-DDEBUG=1), thefprintf(stderr, "error\n");line will be included in the compiled program, printing “error” to the standard error stream. - If
DEBUGis not defined or has a different value (e.g.,0), thefprintfline is excluded from the compiled program, as if it were never written.
3. The Role of the DEBUG Macro
The DEBUG macro is a common convention in C programming. It’s typically used to control whether debug-related code (like logging or error messages) is included. Your teacher is showing you how to:
- Use a macro to toggle debug output.
- Conditionally compile code based on whether debugging is enabled.
For example:
- During development, you might set
DEBUGto1to include diagnostic messages. - In production, you might set
DEBUGto0(or leave it undefined) to exclude these messages, making the program leaner and avoiding unnecessary output.
4. The fprintf(stderr, "error\n") Line
This line uses fprintf to print “error” to stderr (the standard error stream), which is typically used for error messages or diagnostics. The \n ensures a newline for clean output. This is a simple example of debug output that might help you diagnose issues during development.
5. Why This Matters
Your teacher is teaching you how to write flexible code that can behave differently depending on the build configuration. This is a powerful technique because:
- You can add debug code without worrying about it appearing in the final product.
- You can control program behavior (e.g., enabling/disabling features) using compiler flags or macro definitions.
- It introduces you to the preprocessor, which is a fundamental part of C programming.
6. Fixing the Code
The code you provided has a few issues:
- The
®character andtendifare likely typos. The correct directive is#endif. - The stray
3at the end is invalid and would cause a syntax error.
The corrected version (as shown above) is a minimal function that:
- Conditionally prints “error” to
stderrifDEBUGis1. - Always returns
1.
7. How DEBUG Is Set
The DEBUG macro can be defined in several ways:
- In the code: Using
#define DEBUG 1before the#ifdirective. - Via the compiler: Passing a flag like
-DDEBUG=1when compiling (e.g.,gcc -DDEBUG=1 program.c). - In a build system: Tools like
makeor CMake can set macros based on build configurations.
For example, if you compile with DEBUG set to 1, the compiled program includes the fprintf call. If you compile without DEBUG or with DEBUG set to 0, the fprintf is omitted.
8. Example Compilation Scenarios
Assume the corrected code:
#include <stdio.h>
#define DEBUG 1
int bar() {
#if DEBUG == 1
fprintf(stderr, "error\n");
#endif
return 1;
}
int main() {
bar();
return 0;
}- With
DEBUG == 1: Running the program prints “error” tostderrand returns1frombar(). - With
DEBUG == 0(change#define DEBUG 0): Thefprintfline is excluded, so nothing is printed, butbar()still returns1.
If you compile without defining DEBUG (e.g., remove the #define), the #if DEBUG == 1 condition is false (since DEBUG is undefined and treated as 0 in preprocessor arithmetic), so the fprintf is excluded.
9. Broader Lesson
Your teacher is likely building on this to teach you:
- Modular code: Use preprocessor directives to make code adaptable to different scenarios.
- Debugging techniques: Conditionally include diagnostic output to troubleshoot issues.
- Preprocessor mechanics: Understand how the preprocessor manipulates code before compilation.
- Real-world practices: Conditional compilation is widely used in professional C projects (e.g., in libraries, operating systems, or embedded systems).
10. Practice to Reinforce
To deepen your understanding:
- Try compiling the code with and without
DEBUGdefined (e.g., using-DDEBUG=1or-DDEBUG=0withgcc). - Modify the
#ifcondition to check other values (e.g.,#if DEBUG == 2) and observe the behavior. - Add more debug output (e.g., print a variable’s value) inside the
#ifblock. - Experiment with other preprocessor directives like
#ifdef DEBUG(checks ifDEBUGis defined, regardless of its value) or#elseto handle alternative cases.
11. Connection to Pointers (from Your Previous Question)
If this lesson follows your previous question about pointers (arr[3] vs. *(arr + 3)), your teacher might be systematically introducing you to core C concepts:
- Pointers: How memory is accessed and manipulated.
- Preprocessor: How code is conditionally included before compilation.
- These are foundational for writing efficient, flexible, and debuggable C programs.
If you have more questions about this code, the preprocessor, or how it ties into pointers, let me know!
#!/usr/bin/env python3
# hex_diff.py – compute the difference between two hex values (provided as strings)
# usage: python hex_diff.py "0x7ffd0753f1d0" "0x7ffd0753f1dc"
import sys
if __name__ == "__main__":
if len(sys.argv) != 3:
print("usage: python hex_diff.py <hex1> <hex2>")
sys.exit(1)
try:
hex1 = int(sys.argv[1], 16)
hex2 = int(sys.argv[2], 16)
diff = abs(hex2 - hex1)
print("Difference (decimal):", diff)
print("Difference (hex):", hex(diff))
except ValueError as e:
print("Error: invalid hex value –", e)
easy way to diff the hex vaule
#include <stdio.h>
/* Define a debug flag. Set to 0 to disable debug output. */
#define DEBUG 1
/* A debug macro that prints a message (using do-while(0) for safety). */
#define DEBUG_PRINT(msg) \
do { \
if (DEBUG) \
fprintf(stderr, "DEBUG: %s\n", (msg)); \
} while (0)
/* A utility macro to compute the minimum of two values. */
#define MIN(a, b) ((a) < (b) ? (a) : (b))
/* Define a platform flag (e.g., PLATFORM_WINDOWS) for conditional compilation.
*/
#define PLATFORM_WINDOWS 1
#define PLATFORM_LINUX 0
/* Conditional compilation block: define CLEAR_SCREEN based on the platform. */
#if PLATFORM_WINDOWS
#define CLEAR_SCREEN "cls"
#elif PLATFORM_LINUX
#define CLEAR_SCREEN "clear"
#else
#define CLEAR_SCREEN ""
#endif
int main() {
/* Demonstrate debug macro. */
DEBUG_PRINT("Starting program.");
/* Demonstrate utility macro MIN. */
int a = 5, b = 3;
printf("MIN(%d, %d) = %d\n", a, b, MIN(a, b));
/* Demonstrate conditional compilation (e.g., clearing the screen). */
printf("Clearing screen (using CLEAR_SCREEN macro)...\n");
/* Uncomment the next line to actually clear the screen (requires stdlib.h).
*/
/* system(CLEAR_SCREEN); */
DEBUG_PRINT("Program finished.");
return 0;
}
#define DEBUG_PRINT(msg) \
do { \
if (DEBUG) \
fprintf(stderr, "DEBUG: %s\n", (msg)); \
} while (0)
this make the debug fuction happen, debug 1 → enable it , 0 disable
- convince
- A brief overview of structs in C
group all kind of variable
object without method
struct will ofter use the concept of pointer
when you use struct inside fucnction like arg , or return large struct will be copy on stack and it will take time and space
#include <stdio.h>
struct user {
int age;
short postcode;
char *name; // char pointer , struct will user struct int 8 byte pointer field
};
int main() {
struct user u = {25, 10000, "Bob"};
struct user u2 = {17, 20000, "Alice"};
struct user u3 = {17, 20000, "Peter"};
struct user *p = &u3;
printf("%s is %d years old\n", u.name, u.age);
printf("%s is %d years old\n", u2.name, u2.age);
// printf("%s is %d years old\n", p.name); -> this won't work
printf("%s is %d years old\n", (*p).name, (*p).age);
printf("%s is %d years old\n", p->name, p->age);
printf("ok\n");
}
generally, struct is gonna be lay out continuely without space in the order you specific , one thing is about alignment
#include <stdio.h>
struct user {
int age; // 4 bytes
short postcode; // 2bytes
char *name; // char pointer , struct will user struct int 8 byte pointer field
};
int main() {
struct user u = {25, 10000, "Bob"};
struct user u2 = {17, 20000, "Alice"};
struct user u3 = {17, 20000, "Peter"};
struct user *p = &u3;
printf("%s is %d years old\n", u.name, u.age);
printf("%s is %d years old\n", u2.name, u2.age);
// printf("%s is %d years old\n", p.name); -> this won't work
printf("%s is %d years old\n", (*p).name, (*p).age);
printf("%s is %d years old\n", p->name, p->age);
printf("ok\n");
printf(" this is the address of %p %p %p %p\n ", &u, &(u.age), &(u.postcode),
&(u.name));
}
// Bob is 25 years old
// Alice is 17 years old
// Peter is 17 years old
// Peter is 17 years old
// ok
// this is the address of 0x7ffdb4a3d1b0 0x7ffdb4a3d1b0 0x7ffdb4a3d1b4
// 0x7ffdb4a3d1b8
// %
struct user users[2] = {{1, 10000, "foo"}, {2, 10001, "bar"}};
printf("%s is %d years old\n", users[1].name, users[1].age);
c is need to be able to these kind of array in a constant time muiltiple dimensional arrays in c
struct is always in a certain size
printf("One struct is %lu bytes\n", sizeof(struct user));
printf("users array is at %p, \"%s\" is located at %p\n", users,
users[1].name, &users[1].name);
explain how to count 0x7ffe6b1f9ea0 to 0x7ffe6b1f9eb8
users array is at 0x7ffe6b1f9ea0, “bar” is located at 0x7ffe6b1f9eb8
Your teacher is introducing you to structs in C, a fundamental concept for grouping related data, and tying it to other key ideas like pointers, memory layout, arrays, and memory alignment. The code snippets and notes you provided illustrate how structs work, their memory organization, and practical considerations like accessing fields or managing large structs. Below, I’ll explain the concept of structs based on your teacher’s examples, address the memory address calculation (e.g., from 0x7ffe6b1f9ea0 to 0x7ffe6b1f9eb8), and clarify the key lessons your teacher is emphasizing. I’ll keep it concise, practical, and focused on your current learning level, building on your prior questions about pointers and macros.
1. Overview of Structs in C
A struct (short for structure) in C is a user-defined data type that groups variables of different types into a single unit. Think of it as an “object without methods” (as your teacher noted), where you bundle related data together.
Key Characteristics
-
Grouping Variables: A struct combines different types (e.g.,
int,short,char*) into one cohesive type.struct user { int age; // 4 bytes short postcode; // 2 bytes char *name; // 8 bytes (pointer on 64-bit systems) }; -
Contiguous Memory Layout: Struct fields are laid out in memory sequentially in the order declared, though alignment (padding) may add extra bytes for efficiency.
-
Fixed Size: Each struct instance has a predictable size, determined by its fields and alignment (e.g.,
sizeof(struct user)). -
No Methods: Unlike objects in languages like C++ or Java, C structs only hold data, not functions.
-
Pointers and Structs: Structs are often used with pointers for efficiency, especially when passing to functions or returning from them, to avoid copying large data.
Why Structs Are Useful
- Organize related data (e.g., a
userwithage,postcode, andname). - Enable arrays of structs for constant-time access (like
users[1]). - Support complex data structures (e.g., linked lists, trees) when combined with pointers.
2. Key Concepts Your Teacher Is Teaching
Your teacher’s code and notes emphasize several critical aspects of structs, which I’ll explain using the provided examples.
a) Creating and Accessing Structs
You can create struct instances and access their fields using the dot (.) operator:
struct user u = {25, 10000, "Bob"};
printf("%s is %d years old\n", u.name, u.age); // Bob is 25 years old- Initialization:
uis initialized with values forage,postcode, andnamein the order declared. - Dot Operator (
.): Access fields directly (e.g.,u.name).
b) Structs and Pointers
Structs are often used with pointers to avoid copying large data. You access fields through a pointer using:
- Dereference (
*):(*p).namedereferences the pointerpand accesses thenamefield. - Arrow Operator (
->):p->nameis a shorthand for(*p).name.
struct user u3 = {17, 20000, "Peter"};
struct user *p = &u3;
printf("%s is %d years old\n", (*p).name, (*p).age); // Peter is 17 years old
printf("%s is %d years old\n", p->name, p->age); // Peter is 17 years old- Why
p.nameFails:pis a pointer, not a struct, sop.nameis invalid. You must dereference ((*p).name) or use->(p->name). - Lesson: Pointers are common with structs for efficiency and flexibility, especially in functions or dynamic memory allocation.
c) Memory Layout and Alignment
Struct fields are laid out contiguously in memory, but alignment may add padding to ensure fields align with memory boundaries (e.g., 4-byte or 8-byte boundaries for performance).
struct user {
int age; // 4 bytes
short postcode; // 2 bytes + 2 bytes padding (to align next field)
char *name; // 8 bytes
};-
Size Calculation:
int age: 4 bytes.short postcode: 2 bytes, but compilers often add 2 bytes of padding to align the next field (name) on an 8-byte boundary (common on 64-bit systems).char *name: 8 bytes (pointer size on 64-bit systems).- Total:
4 + 2 + 2 + 8 = 16 bytes(confirmed withsizeof(struct user)).
-
Example Output:
printf("One struct is %lu bytes\n", sizeof(struct user)); // One struct is 16 bytes -
Memory Addresses:
printf("this is the address of %p %p %p %p\n", &u, &(u.age), &(u.postcode), &(u.name)); // Output: 0x7ffdb4a3d1b0 0x7ffdb4a3d1b0 0x7ffdb4a3d1b4 0x7ffdb4a3d1b8&uand&(u.age)are the same (base address of the struct).&(u.postcode)is at0x7ffdb4a3d1b4(base + 4 bytes).&(u.name)is at0x7ffdb4a3d1b8(base + 4 + 2 + 2 = 8 bytes).
-
Lesson: Structs are laid out sequentially, but padding ensures alignment, affecting the total size and field offsets.
d) Arrays of Structs
Structs can be stored in arrays, allowing constant-time access with indexing:
struct user users[2] = {{1, 10000, "foo"}, {2, 10001, "bar"}};
printf("%s is %d years old\n", users[1].name, users[1].age); // bar is 2 years old- Memory Layout:
users[0]starts at the array’s base address (e.g.,0x7ffe6b1f9ea0).users[1]is atbase + sizeof(struct user)(e.g.,0x7ffe6b1f9ea0 + 16 = 0x7ffe6b1f9eb0).
- Constant-Time Access:
users[i]computes the address asbase + i * sizeof(struct user), enabling fast access. - Lesson: Arrays of structs are efficient for managing collections of structured data.
e) Passing Structs to Functions
Your teacher noted that passing large structs to functions or returning them copies the entire struct onto the stack, which is slow and memory-intensive:
void print_user(struct user u) {
printf("%s is %d years old\n", u.name, u.age);
}- Problem:
uis copied (16 bytes forstruct user), which is inefficient for large structs. - Solution: Pass a pointer instead:
void print_user(struct user *u) {
printf("%s is %d years old\n", u->name, u->age);
}- Why: Only the pointer (8 bytes) is copied, and
->accesses fields efficiently. - Lesson: Use pointers to structs in functions to save time and space.
3. Memory Address Calculation: 0x7ffe6b1f9ea0 to 0x7ffe6b1f9eb8
Your teacher’s example shows:
users array is at 0x7ffe6b1f9ea0, "bar" is located at 0x7ffe6b1f9eb8
x python hex_diff.py “0x7ffe6b1f9ea0” “0x7ffe6b1f9eb8” Difference (decimal): 24 Difference (hex): 0x18
This refers to the address of the users array and the address of users[1].name (the name field of users[1]). Let’s calculate the difference and explain why it’s 0x7ffe6b1f9eb8.
Step-by-Step Calculation
-
Array Base Address:
usersis at0x7ffe6b1f9ea0.users[0]starts at0x7ffe6b1f9ea0.users[1]starts at0x7ffe6b1f9ea0 + sizeof(struct user) = 0x7ffe6b1f9ea0 + 16 = 0x7ffe6b1f9eb0.
-
Struct Layout:
- Inside
users[1]:age: 4 bytes (offset 0:0x7ffe6b1f9eb0).postcode: 2 bytes + 2 bytes padding (offset 4:0x7ffe6b1f9eb4).name: 8 bytes (offset 8:0x7ffe6b1f9eb8).
&users[1].nameis atusers[1] base + 8 = 0x7ffe6b1f9eb0 + 8 = 0x7ffe6b1f9eb8.
- Inside
-
Hex Arithmetic:
0x7ffe6b1f9ea0(array base).- Add
16(0x10 in hex) forusers[1]:0x7ffe6b1f9ea0 + 0x10 = 0x7ffe6b1f9eb0. - Add
8(offset ofname):0x7ffe6b1f9eb0 + 0x8 = 0x7ffe6b1f9eb8. - Result:
0x7ffe6b1f9eb8, matching&users[1].name.
-
Why This Matters:
- The difference (
0x7ffe6b1f9eb8 - 0x7ffe6b1f9ea0 = 0x18or 24 bytes) shows:- 16 bytes for
users[0](entirestruct user). - 8 bytes to reach the
namefield inusers[1].
- 16 bytes for
- This demonstrates how structs and arrays are laid out in memory, with predictable offsets.
- The difference (
Lesson
- Struct fields have fixed offsets, determined by their order and alignment.
- Arrays of structs are contiguous, with each element offset by
sizeof(struct). - Pointer arithmetic (e.g.,
users + 1) computes addresses based onsizeof(struct user).
4. Broader Lessons from Your Teacher
Your teacher is building a foundation for understanding how C manages data and memory:
- Structs as Data Containers: Group related data for clarity and organization.
- Memory Layout: Structs are contiguous, but alignment adds padding, affecting size and field offsets.
- Pointers and Efficiency: Use pointers to structs for functions, dynamic allocation, or large data to avoid copying.
- Arrays and Constant-Time Access: Struct arrays enable fast, indexed access, critical for data structures.
- Practical Considerations: Understand memory addresses and sizes (
sizeof) for debugging and optimization.
Connection to Previous Questions
-
Pointers: Your earlier question about
arr[3]vs.*(arr + 3)ties to structs. Struct arrays (users[i]) use similar pointer arithmetic, and->is a pointer-based access method. -
Macros: You could use macros to simplify struct operations, e.g.:
#define PRINT_USER(u) printf("%s is %d years old\n", (u)->name, (u)->age)This works for both
PRINT_USER(&u)andPRINT_USER(p).
5. Practice to Reinforce
To solidify these concepts:
-
Size and Alignment: Use
sizeofto check the size of different structs. Reorder fields (e.g.,char*,int,short) and observe padding changes. -
Pointer Access: Write a function that takes a
struct user*and prints its fields using->. -
Array Iteration: Loop over a
struct userarray and print all users.for (int i = 0; i < 2; i++) { printf("%s\n", users[i].name); } -
Address Arithmetic: Print addresses of all fields in
users[0]andusers[1]to confirm offsets. -
Dynamic Allocation: Create a
struct userdynamically withmallocand access it via a pointer.
6. Key Takeaways
- Structs group variables into a single type, laid out contiguously with possible padding for alignment.
- Pointers are essential for efficient struct handling (e.g.,
->, passing to functions). - Arrays of structs enable fast access and are stored contiguously.
- Memory Layout: Understand
sizeof, field offsets, and alignment for debugging and optimization. - Practical Use: Structs are the backbone of complex data structures and real-world C programs.
If you want more examples, clarification on alignment, or help with a specific struct-related task (e.g., multi-dimensional arrays, dynamic allocation), let me know!
#include <stdio.h>
// Define a simple struct to represent a student
struct student {
int id; // 4 bytes
short grade; // 2 bytes + 2 bytes padding
char *name; // 8 bytes on 64-bit systems
}; // Total: 16 bytes
int main() {
// Create an array of 2 students
struct student students[2] = {{1001, 85, "Alice"}, {1002, 92, "Bob"}};
// Print the size of the struct and array
printf("Size of struct student: %lu bytes\n", sizeof(struct student));
printf("Size of students array: %lu bytes\n", sizeof(students));
// Print base address of array and first student
printf("\nArray base address: %p\n", (void *)students);
printf("First student address: %p\n", (void *)&students[0]);
// Access using array notation
printf("\nUsing array notation:\n");
printf("Student 1: %s (ID: %d, Grade: %d)\n", students[0].name,
students[0].id, students[0].grade);
// Access using pointer notation
struct student *ptr = &students[1];
printf("\nUsing pointer notation:\n");
printf("Student 2: %s (ID: %d, Grade: %d)\n", ptr->name, ptr->id, ptr->grade);
// Show field addresses for first student
printf("\nField addresses for first student:\n");
printf("id field: %p\n", (void *)&students[0].id);
printf("grade field: %p\n", (void *)&students[0].grade);
printf("name field: %p\n", (void *)&students[0].name);
return 0;
}
// Size of struct student: 16 bytes
// Size of students array: 32 bytes
//
// Array base address: 0x7ffc5859c1d0
// First student address: 0x7ffc5859c1d0
//
// Using array notation:
// Student 1: Alice (ID: 1001, Grade: 85)
//
// Using pointer notation:
// Student 2: Bob (ID: 1002, Grade: 92)
//
// Field addresses for first student:
// id field: 0x7ffc5859c1d0
// grade field: 0x7ffc5859c1d4- think before putting struct in functino , depends on situation
- The generic pointer (void *) in C (16:21)
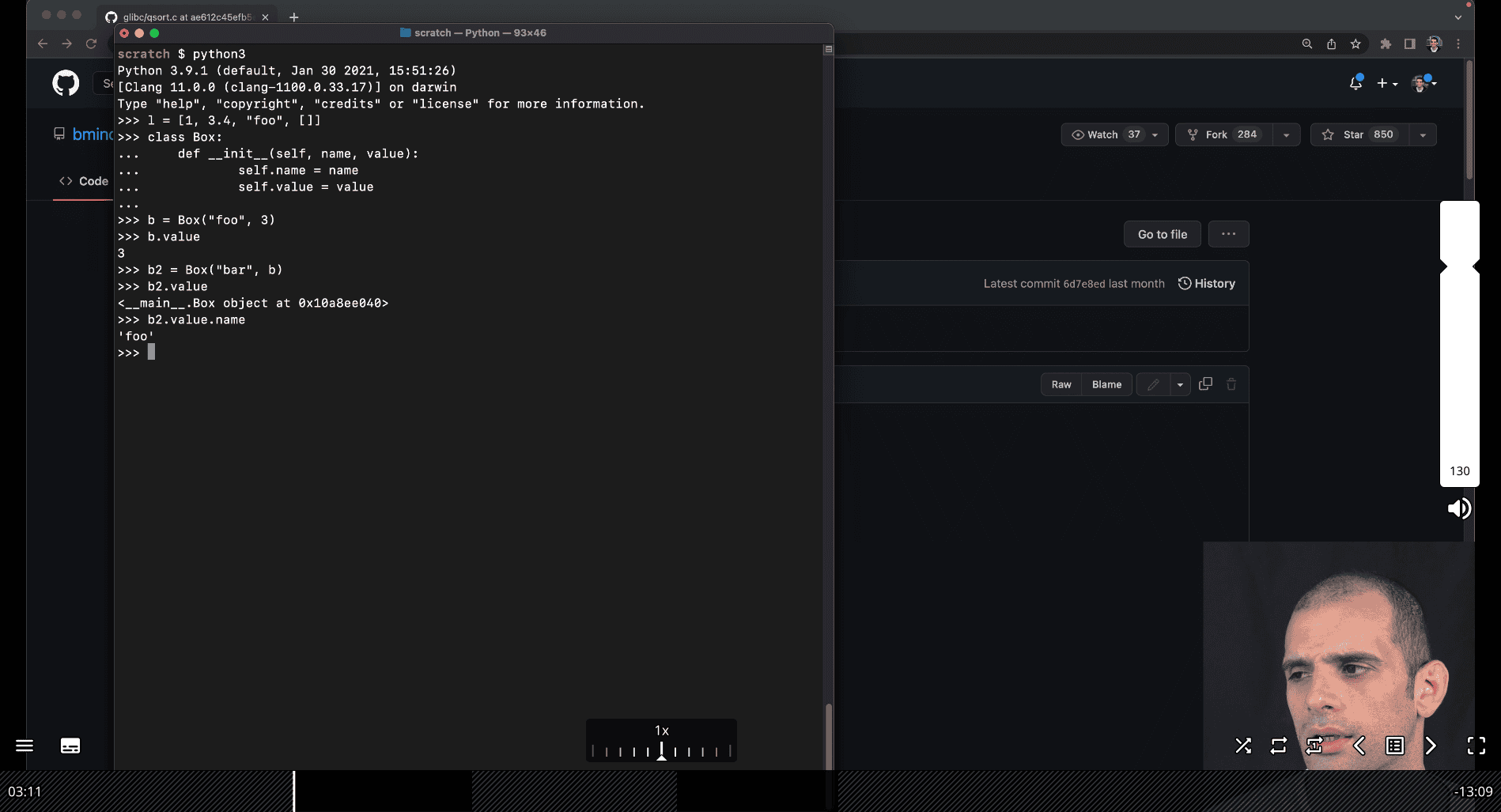
 To address your question, let’s assume that the context is translating the Python
To address your question, let’s assume that the context is translating the Python Box class scenario into C, where b2 is an object (or struct) similar to the Python example, and we are dealing with pointers and type casting. In C, b2.value would likely be a pointer or a field in a struct, and you’re asking about the expressions *(int*)b2.value and (int*)b2.value. Let’s break this down clearly.
Context Setup
Assume we have a C struct analogous to the Python Box class:
typedef struct Box {
char* name; // String for the name
void* value; // Generic pointer for the value (to mimic Python's flexibility)
} Box;Suppose:
bis aBoxstruct withname = "foo"andvaluepointing to an integer (e.g.,3).b2is aBoxstruct withname = "bar"andvaluepointing tob(i.e.,b2.valueholds the address of theBoxstructb).
Example initialization:
Box b = {"foo", malloc(sizeof(int))}; // Allocate memory for an int
*(int*)b.value = 3; // Store 3 in the allocated memory
Box b2 = {"bar", &b}; // b2.value points to bNow, let’s evaluate the expressions *(int*)b2.value and (int*)b2.value.
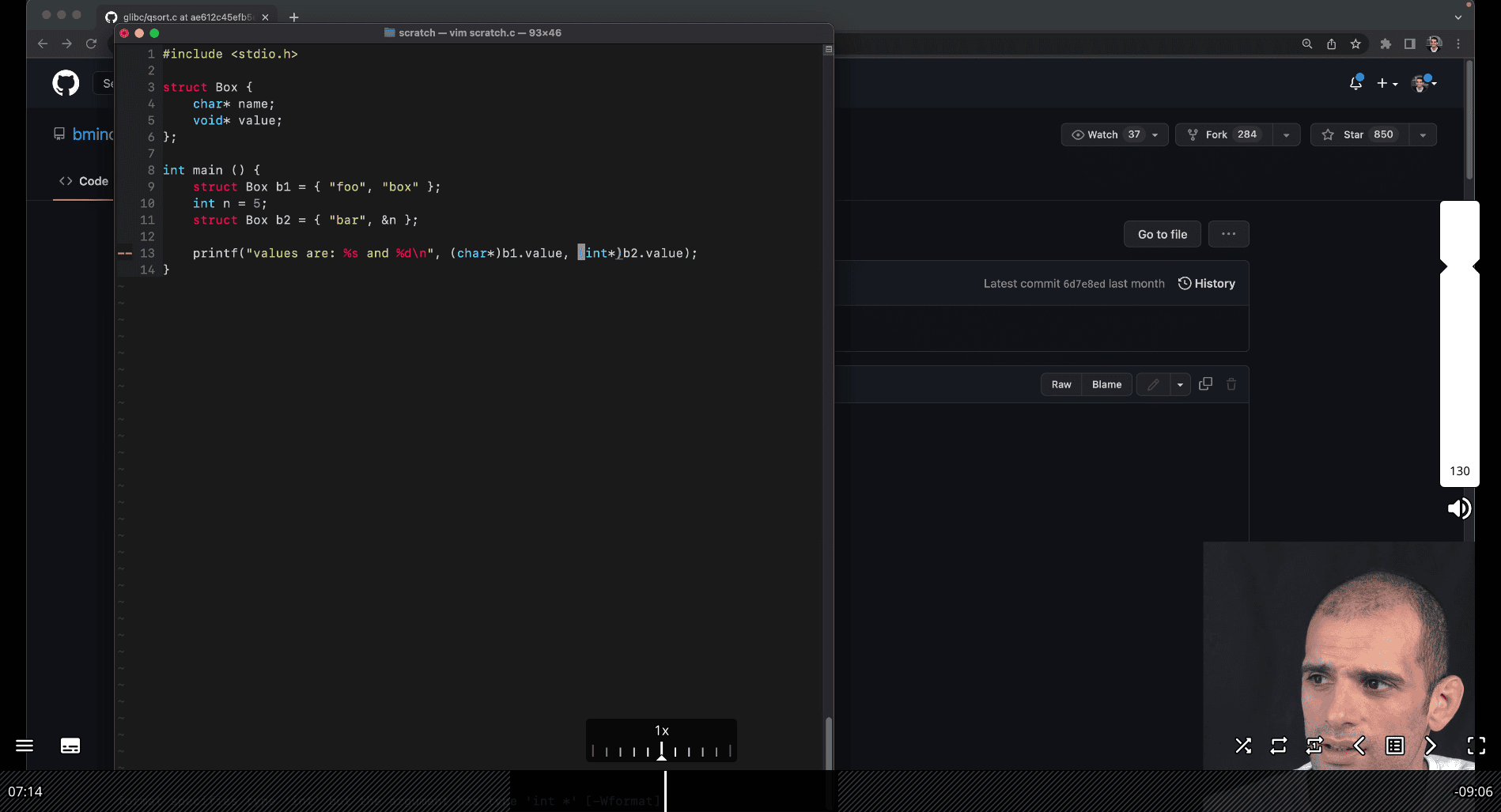
1. (int*)b2.value
- What it does: This is a type cast of
b2.valueto a pointer to an integer (int*). - Explanation:
b2.valueis avoid*(in our struct definition), which holds the address of theBoxstructb.- Casting it to
int*with(int*)b2.valuetells the compiler to treat the address stored inb2.valueas if it points to an integer. - The result is an
int*(a pointer to an integer), but it does not dereference the pointer—it simply reinterprets the address.
- Value: The address of
b(i.e.,&b), but now typed asint*instead ofvoid*. - Correctness: This cast is generally unsafe because
b2.valuepoints to aBoxstruct, not an integer. Treating the starting address of aBoxstruct as anint*could lead to undefined behavior if you try to use it, as the memory layout of aBoxstruct (starting with achar*forname) is not the same as anint.
2. *(int*)b2.value
- What it does: This expression first casts
b2.valueto anint*(as above) and then dereferences the resulting pointer to access the integer value at that address. - Explanation:
- As with
(int*)b2.value,(int*)b2.valuecastsb2.value(which is&b) to anint*. - The
*operator then tries to dereference thisint*to retrieve the integer value at the address&b. - Since
&bis the address of aBoxstruct, dereferencing it as anintassumes the firstsizeof(int)bytes of theBoxstruct represent an integer, which is incorrect and leads to undefined behavior.
- As with
- Value: The result is undefined because the memory at
&bcontains aBoxstruct (starting with achar*forname), not an integer. The program might crash, return garbage data, or behave unpredictably. - Correctness: This operation is invalid in this context because
b2.valuepoints to aBoxstruct, not an integer.
Key Difference
-
(int*)b2.value:- Returns a pointer (
int*) by castingb2.valueto anint*. - It does not access the memory at that address; it only changes the type of the pointer.
- Result: The address
&b, typed asint*. - Use case: You might use this if you need to pass the address to a function expecting an
int*, but in this case, the cast is unsafe unlessb2.valueactually points to an integer.
- Returns a pointer (
-
*(int*)b2.value:- Dereferences the casted pointer to access the value at the address.
- Attempts to interpret the memory at
&bas an integer, which is invalid in this context and causes undefined behavior. - Result: Undefined (likely garbage or a crash).
- Use case: This would only be valid if
b2.valuepointed to an actual integer, which it does not in this scenario.
Why This Happens
In the Python example, b2.value is the Box object b, and b2.value.name accesses b’s name field ("foo"). In C, b2.value is a pointer to the Box struct b. If you want to access b’s name field in C, you would use:
((Box*)b2.value)->nameThis casts b2.value to a Box* (since it points to a Box struct) and accesses the name field, which would return "foo".
However, both (int*)b2.value and *(int*)b2.value are incorrect in this context because they assume b2.value points to an integer, when it actually points to a Box struct.
Correct Approach
If you intended to access the integer value stored in b.value (i.e., 3), you would need to:
- Cast
b2.valueto aBox*to access theBoxstructb. - Then access
b.valueand cast that to anint*to get the integer.
For example:
*(int*)((Box*)b2.value)->valueb2.valueis&b(avoid*pointing to aBox).(Box*)b2.valuecasts it to aBox*.((Box*)b2.value)->valueaccessesb.value, which is avoid*pointing to an integer.(int*)((Box*)b2.value)->valuecastsb.valueto anint*.*(int*)((Box*)b2.value)->valuedereferences to get the integer3.
Summary
(int*)b2.value: Castsb2.valueto anint*, giving a pointer to&btyped asint*. Unsafe in this context.*(int*)b2.value: Dereferences the casted pointer, attempting to read an integer from&b, which causes undefined behavior.- To access
b’sname("foo") in C, use((Box*)b2.value)->name. - To access
b’svalue(3), use*(int*)((Box*)b2.value)->value.
If you have a specific C code snippet or further details about the struct definition, I can refine this explanation!
The Correct Way to Get the Value 3
Here’s the safe way to get the 3 out of the nested structure:
(int)((Box*)b2.value)→value
Let’s walk through it:
b2.value → points to b
(Box*)b2.value → cast it back to a pointer to Box
((Box*)b2.value)->value → go into that Box, get its value field (which points to the int 3)
(int*)... → cast that to an int*
*... → dereference it to get the value 3
💡 Final Analogy
Imagine:
b2 is a box holding another box (b)
b holds a slip of paper with the number 3
To get 3, you must:
Open b2 → find b
Open b → find the paper
Read the paper → get 3
In code:
*(int*)((Box*)b2.value)->value → this is for python example in c, point to another object value in c using
dereference and pointer and value type
A brief tour of LLDB (33:26) useful skils debugging
- thinking about program execution , how this change my program state, memory change , machine change, no bug to hide
stepping through and be patient
super power
print statement can also do that, debuging he mentioned here is more like a step by step
 using lldb → inside → help → help br
using lldb → inside → help → help br
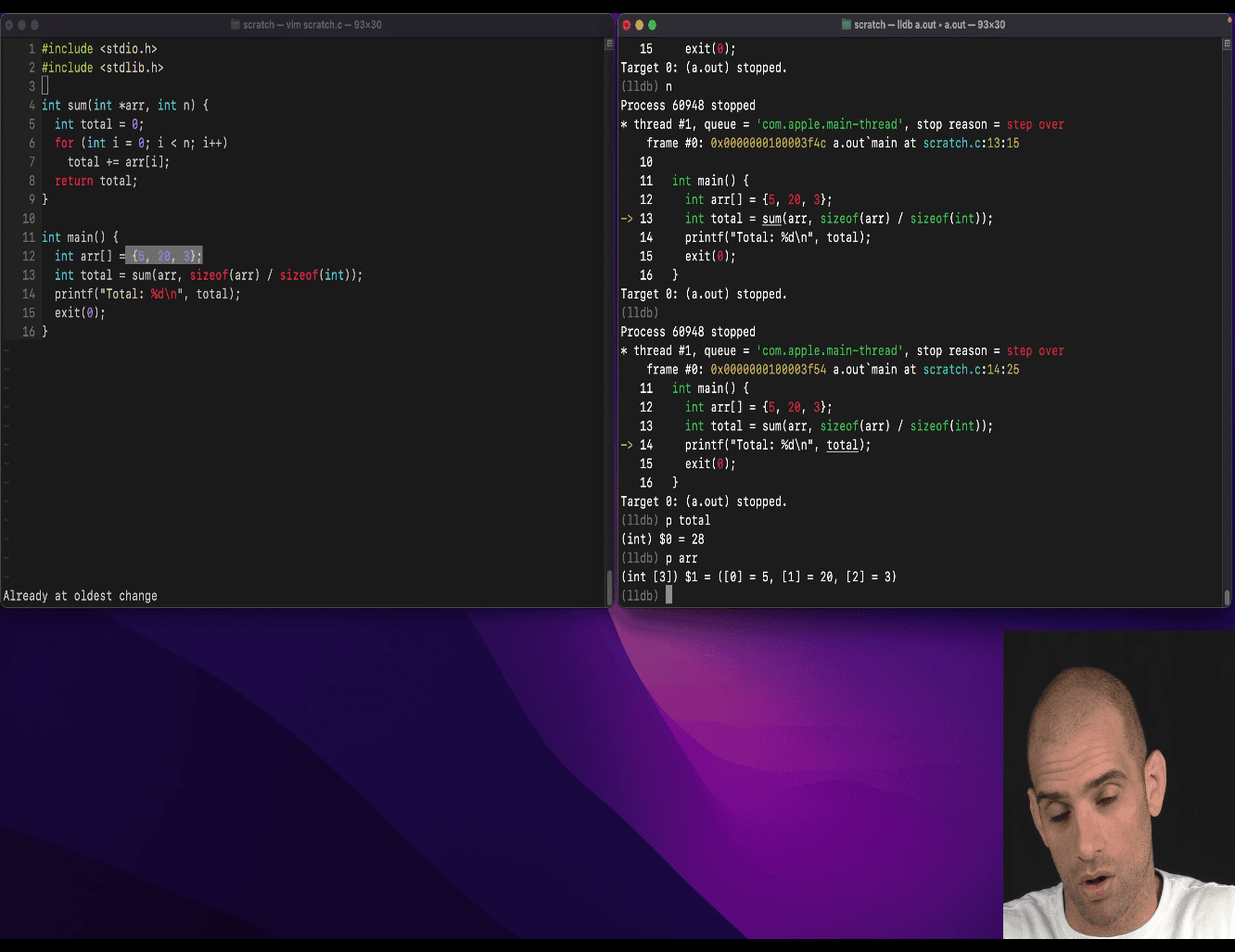
break point main p →print fr select → show current select framework
fr v → show all the variable in the current frame
r → rerun
s → step → more detail dig in
step & print → loop n times display total → step until stop hook disassemble (dis -f (frame))
- dis -f -m(map)
reg(register ) re (read) eax
where you are in the stack: bt (backtrace)
- tracking what frame you on
- checking other frame as well
power tool → need practice
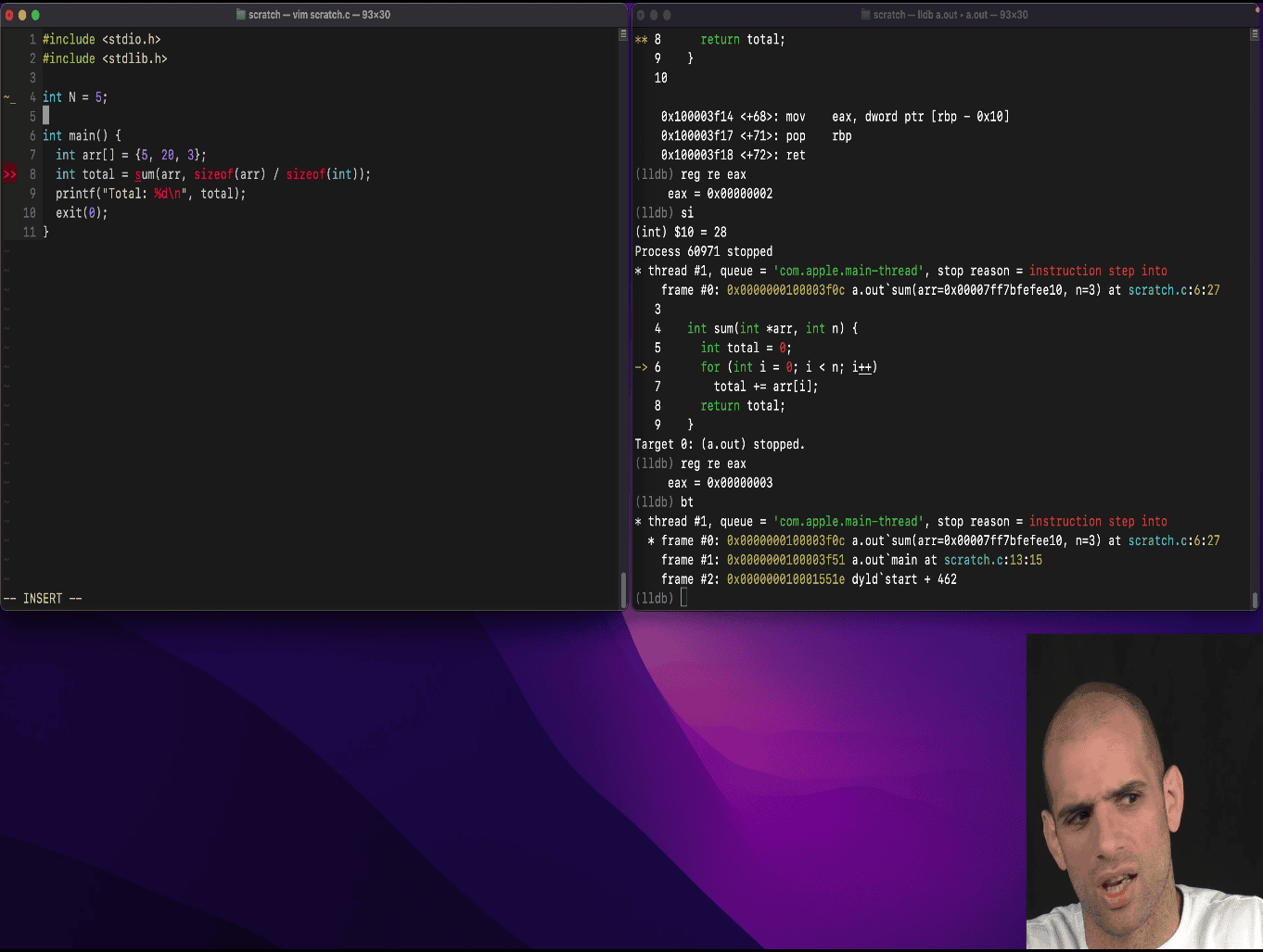
- global variable → lldb → look for memory
where N is being change
watchpoint
w s v N, (watchpoint set variable ‘N’)
c (continue until another breakpoint or watchpoint)
most of the time you won’t know seting watchpoint in specific variable name but more in memory , changes?
e.g. expression, memory Notes on LLDB Watchpoints
Watchpoints only work on variables that are in memory—not registers or optimized-out variables.
They’re limited in number (hardware-supported).
May cause performance issues if the variable is frequently modified.
Great — you’re digging into the core point your teacher is trying to make, which is understanding why buffer overflows overwrite other variables on the stack. Let’s explain exactly why this overwriting happens, and why it’s so dangerous and subtle.
🧠 What Your Teacher Is Teaching
How stack memory works, and how writing beyond bounds (like
arr[4]) can overwrite nearby variables likef.aorf.b.
🔍 Stack Memory Layout (Key Idea)
When your program runs, local variables like arr and f are stored on the stack in memory.
The stack is a contiguous block of memory, and the compiler decides how variables are laid out.
Example
You wrote:
struct foo f = {1, 2}; // 8 bytes (2 ints)
int arr[] = {5, 20, 3}; // 12 bytes (3 ints)arr[0]is at address0x308arr[1]is at0x30carr[2]is at0x310arr[3]is undefinedarr[4]is at0x318
But f starts at 0x314!
So:
0x308: arr[0]
0x30c: arr[1]
0x310: arr[2]
0x314: f.a 👈 gets overwritten!
0x318: f.b 👈 you're writing 90 here!That means
arr[4] = 90actually writes tof.b, possibly even smashingf.ain some compiler configurations.
💥 Why Overwriting Happens
1. Arrays don’t have bounds checking in C
C just lets you do:
arr[4] = 90;Even though the array only has 3 elements, C doesn’t stop you. It simply computes:
*(arr + 4) = 90; // Writes 90 to memory 16 bytes after arr[0]2. Memory is Reused on the Stack
Variables like arr and f are laid out next to each other in memory, like:
[ arr[0] ][ arr[1] ][ arr[2] ][ maybe padding ][ f.a ][ f.b ]If you write beyond arr, you literally write into the space used by f.
3. No Protection or Warning
Unless you use tools like AddressSanitizer, C won’t warn you or protect you.
✅ What Your Teacher’s Trying to Teach
When you write out of bounds (
arr[4] = 90), you’re not just “doing something wrong”, you’re potentially corrupting another variable. Even worse — sometimes this works “fine” and you won’t notice. That makes it harder to debug and dangerous in real systems.
🧪 Why This Is “A Small Chance” Case
Because the memory layout on the stack depends on the compiler, optimization settings, and how variables are arranged:
- Maybe
fcomes afterarr(like in your case) - Maybe
fcomes beforearr(no overwrite) - Maybe there’s padding (nothing gets hit)
- Maybe
f.aorf.bgets corrupted
So whether
arr[4] = 90overwritesf.ais a coincidence of stack layout — that’s why your teacher said “small chance”.
🧠 Takeaway Message
C lets you shoot yourself in the foot. Writing outside of an array:
- Corrupts nearby variables
- Is invisible unless you’re looking carefully
- Creates dangerous, hidden bugs
That’s why this example is so important. He’s teaching you to respect memory boundaries, and understand how the stack works, not just memorize rules.
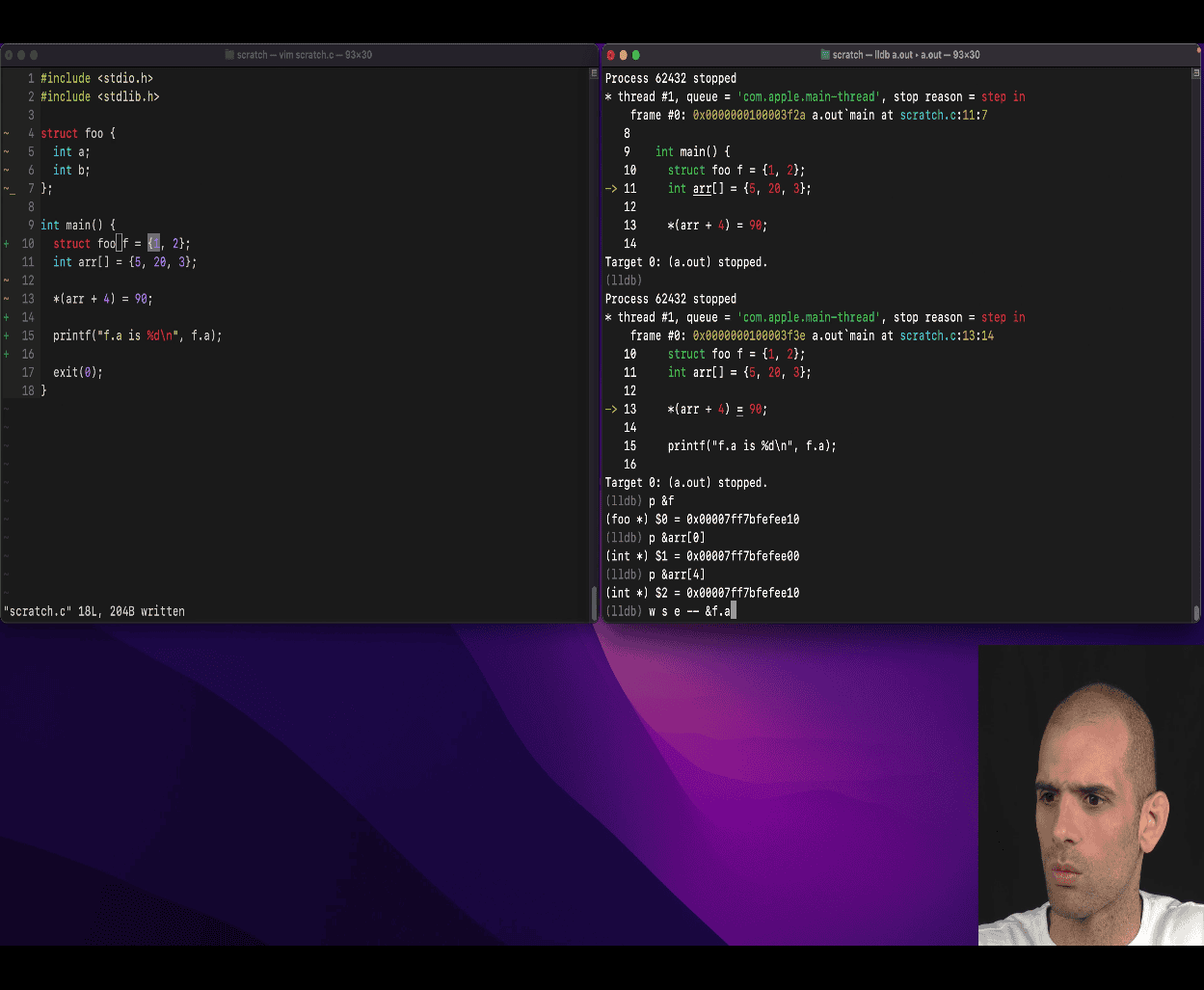 watch that located of memory by anyone who change /write it
watch that located of memory by anyone who change /write it
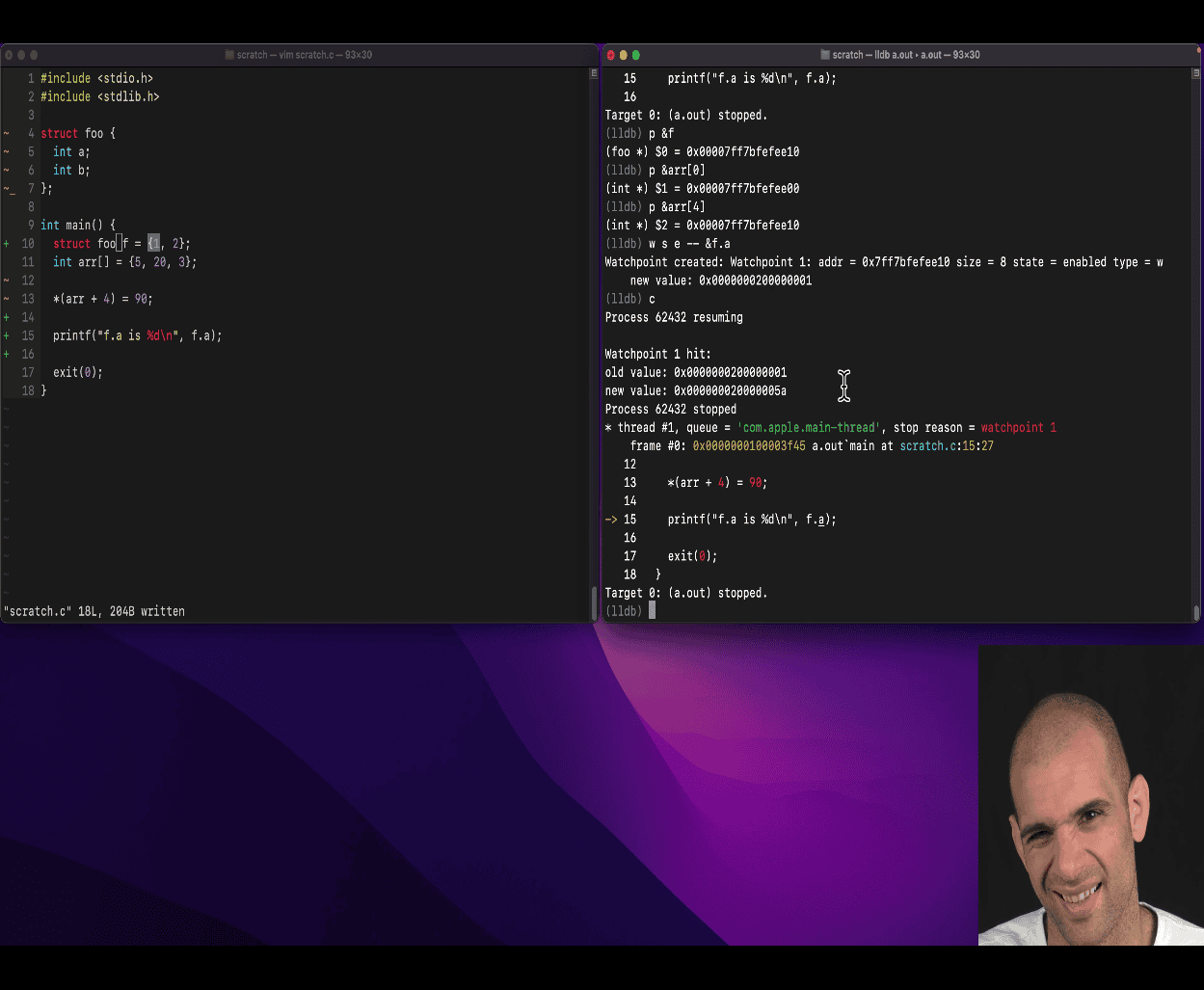
without lldb -g , still using lldb to reverse’eng:
using reg re and regsiter read -all
list main list
stack more info:
📦 What Is the Stack?
The stack is a region of memory used for:
- Function call bookkeeping
- Local variables
- Passing function arguments
It’s called a “stack” because it behaves like a stack data structure: Last In, First Out (LIFO).
📐 Key Characteristics of the Stack
| Feature | Description |
|---|---|
| Grows downward | Stack starts at high memory and grows to lower memory addresses |
| Fast | Access to stack memory is very fast (compared to heap) |
| Automatic | Allocated automatically when a function is called, cleaned up when it returns |
| Contiguous | Memory for each function is laid out in a single, continuous region |
🧱 Stack Frame Layout (per function call)
When you call a function, the program creates a stack frame. Each stack frame contains:
- Return address (where to return after function ends)
- Saved registers (e.g., base pointer)
- Local variables
- Function arguments (sometimes passed in registers instead)
🧪 Example: Stack Frame Visualization
Let’s say you have this:
int main() {
int a = 1;
int b = 2;
int arr[3] = {5, 10, 15};
return 0;
}A simplified view of the stack (assuming no padding) might look like this:
Stack (grows downward)
-------------------------
| arr[2] = 15 | ← lower memory
| arr[1] = 10 |
| arr[0] = 5 |
| b = 2 |
| a = 1 |
-------------------------
↑ high memory
But this order is chosen by the compiler. It could also be:
| a = 1 |
| b = 2 |
| arr[0] = 5 |
| arr[1] = 10 |
| arr[2] = 15 |
Or with padding for alignment (e.g., 8-byte alignment on 64-bit systems), it could look different.
🤯 Why Memory Bugs Happen
Because the compiler decides the order of local variables, if you write beyond the bounds of arr, like:
arr[3] = 999;You’re writing into whatever is laid out after arr, which could be b, a, or some saved register or return address — corrupting the program.
🎯 What Your Teacher Is Demonstrating
Your teacher wants you to understand that:
- Variables are not isolated boxes. They live side-by-side on the stack.
- Array bounds aren’t checked in C, so writing beyond the end affects what comes after it.
- The compiler controls layout, so bugs might not show every time (which makes them dangerous).
- Memory corruption can be subtle, and is often only caught by debugging tools like LLDB or ASan.
This is especially important if you plan to do:
- Systems programming
- Embedded programming
- Security (buffer overflows = exploits!)
- Debugging mysterious crashes
🛡️ Tools to Catch These Bugs
valgrind— detects invalid memory accessAddressSanitizer(-fsanitize=address)lldbwatchpoints or stepping- Compiler warnings:
-Wall -Wextra -Werror
👣 Summary
- The stack is a contiguous, compiler-managed memory block used for local variables and function calls.
- Local variables are laid out adjacent to each other, so an out-of-bounds write can corrupt another variable.
- This is undefined behavior, and your program might silently break, crash, or leak data.
- Your teacher is helping you build intuition about memory layout — a critical foundation for good C programming and debugging.
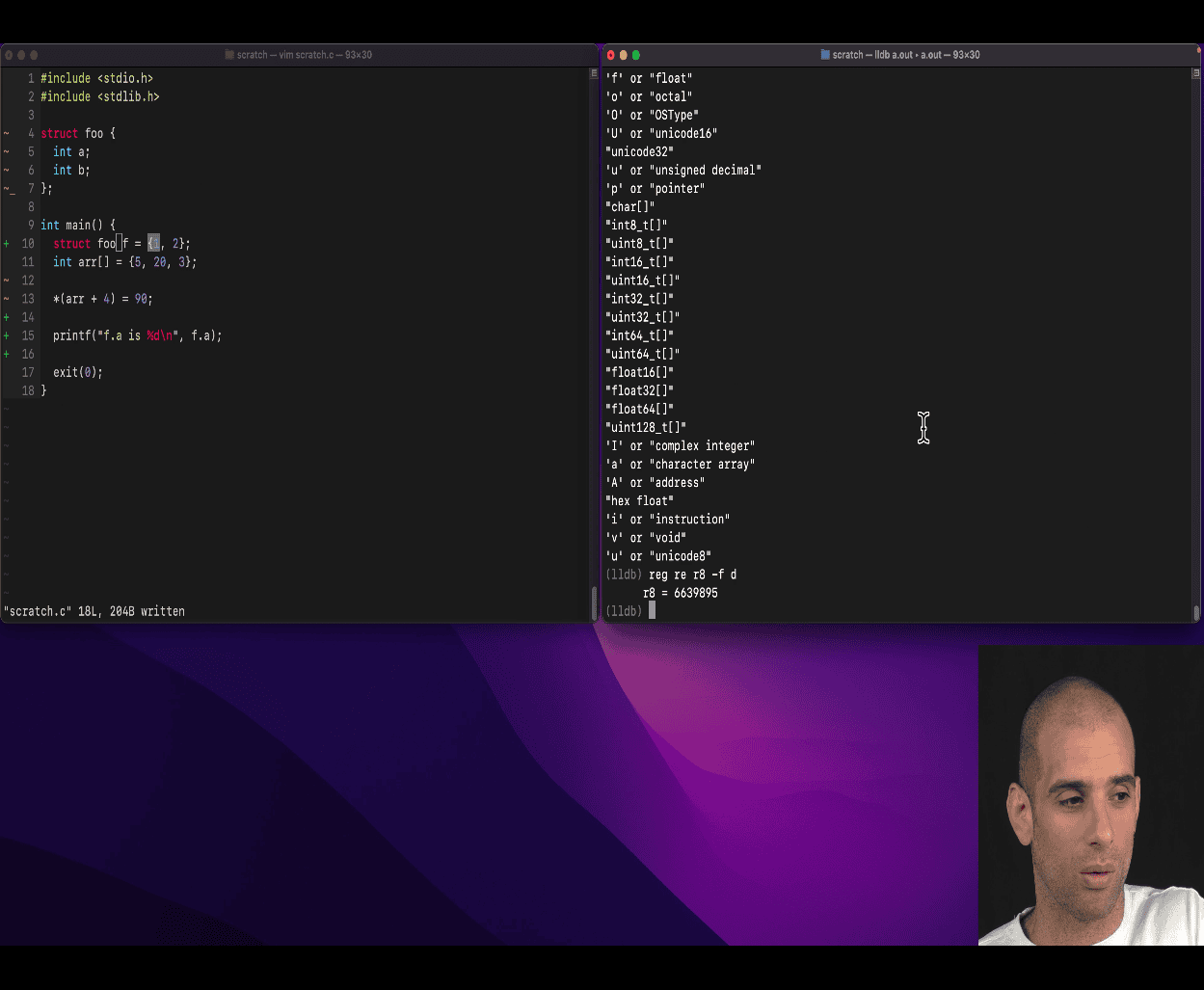 reg re r8 -f d (format ) as d (decimal )
reg re r8 -f d (format ) as d (decimal )
reg re rsp (stack) using this as memory read
mem read $rsp
mem read $rsp-32
Yes — your teacher is absolutely right: Using commands like
mem read $rsp
mem read $rsp - 32is very useful, especially when you’re inspecting the stack frame during debugging or reverse engineering.
Let’s break down exactly what’s going on and why this is powerful.
🧠 What Is $rsp?
$rsp is the stack pointer register on x86_64 systems.
- It points to the top of the stack (the most recent function call’s stack frame).
- Stack memory typically grows downward (from high addresses to low addresses).
🔍 What Does This Do?
1. mem read $rsp
🔎 This reads and dumps memory starting at the current stack pointer.
You’re looking at:
- Local variables (if they’re close to the top)
- Return addresses
- Saved registers
2. mem read $rsp - 32
🔎 This reads memory just above the stack pointer (i.e., from earlier in memory).
This is helpful because:
- Some local variables are placed above the current
$rspvalue (because the compiler might allocate space before moving the stack pointer). - It lets you look into the “past” stack content — maybe even caller function info.
📐 Why It’s Useful
✅ 1. Find Function Arguments, Locals, and Return Addresses
Inspect stack memory around $rsp to see how things are laid out:
^ higher addresses (older data)
|
| [ arr[2] ]
| [ arr[1] ]
| [ arr[0] ]
| [ saved rbp ]
$RSP → | [ return address ]
v lower addressesYou can trace:
- Where variables live in memory
- What values are passed
- What got overwritten (e.g. by buffer overflow)
✅ 2. Catch Bugs or Corruptions
Imagine you accidentally write arr[10] = 99;
Then use:
mem read $rsp
mem read $rsp - 32You might see what was overwritten — even if it’s outside your declared array.
✅ 3. Manually Reconstruct the Stack Frame
Without debug symbols, this is your way of reconstructing:
- What’s on the stack
- What values correspond to which variables
- Which values might be function arguments or return addresses
This is why reverse engineers and security researchers do this all the time.
🔧 Try It Yourself
Write a C program:
#include <stdio.h>
void foo(int x) {
int a = 5;
int b = 10;
int arr[3] = {1, 2, 3};
a = 100; // Change a to see it in stack
b = 200;
arr[0] = 11;
arr[1] = 22;
arr[2] = 33;
printf("Done\n"); // Set a breakpoint here
}
int main() {
foo(999);
return 0;
}Compile without -g, run LLDB, break at foo, and try:
(lldb) reg read rsp
(lldb) mem read $rsp
(lldb) mem read $rsp - 32
(lldb) mem read $rsp + 32You’ll start seeing values match your variables — and really understand the stack.
🧭 Summary
$rsppoints to top of the stack.mem read $rspshows you current stack contents.mem read $rsp - 32shows you memory above the stack (older values or locals).- It’s a powerful technique for inspecting function state, catching overflows, and reverse engineering.
You’re learning how to inspect programs like a CPU debugger or hacker. Keep going — this is foundational knowledge for systems programming, debugging, and security.
Would you like a simple visual diagram showing how stack variables are laid out relative to $rsp?
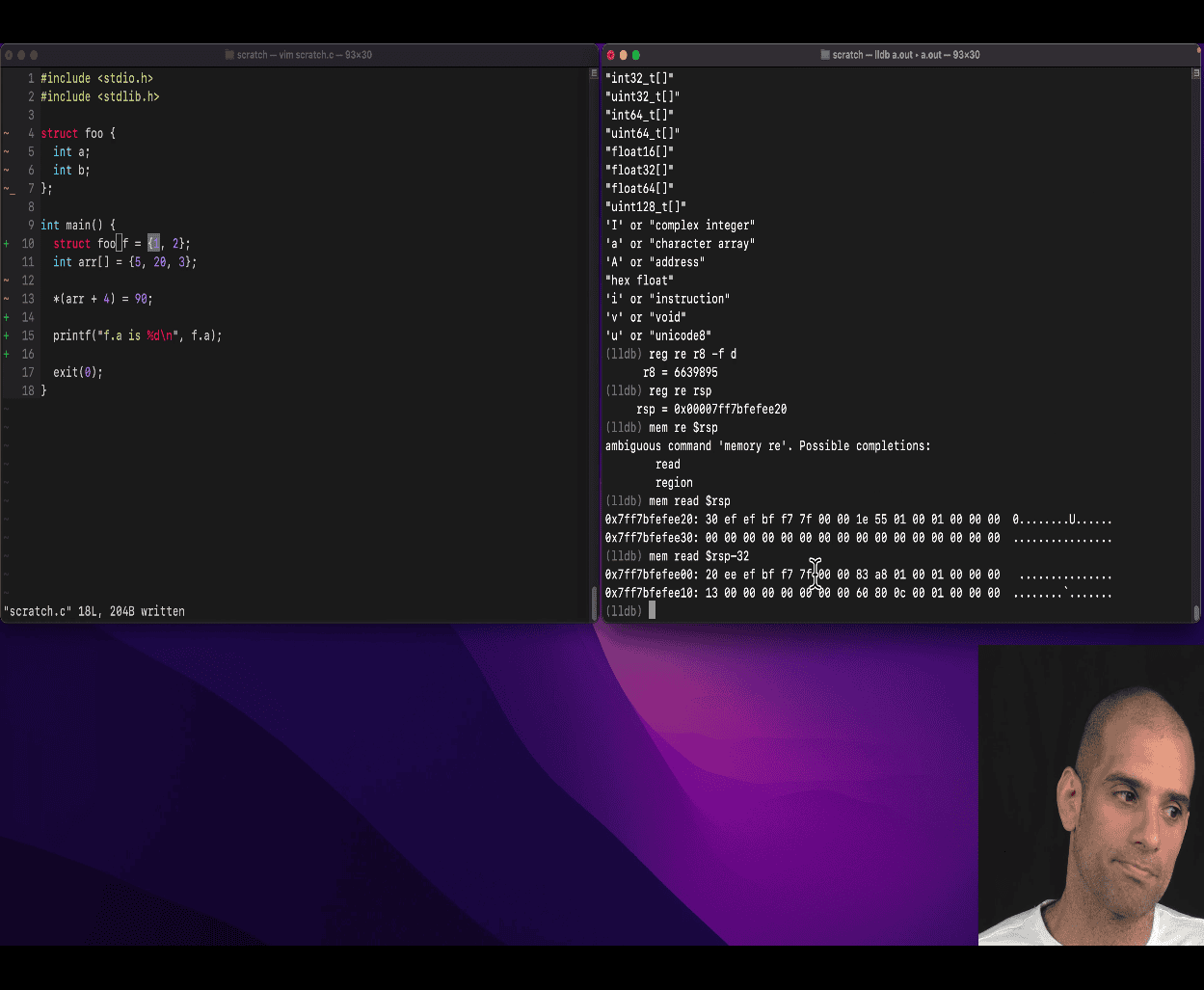
- this is actually funny, I want to learn it later
Helping Jessica understand void** (39:35)
steps → to get the value
int x = 5; → x → 5, x → memory address → contain value 5 in hex 32 bits
int *y = &x; pointer → address of x (aka referencing)
and there is a value , the value is y (on the stack (register))
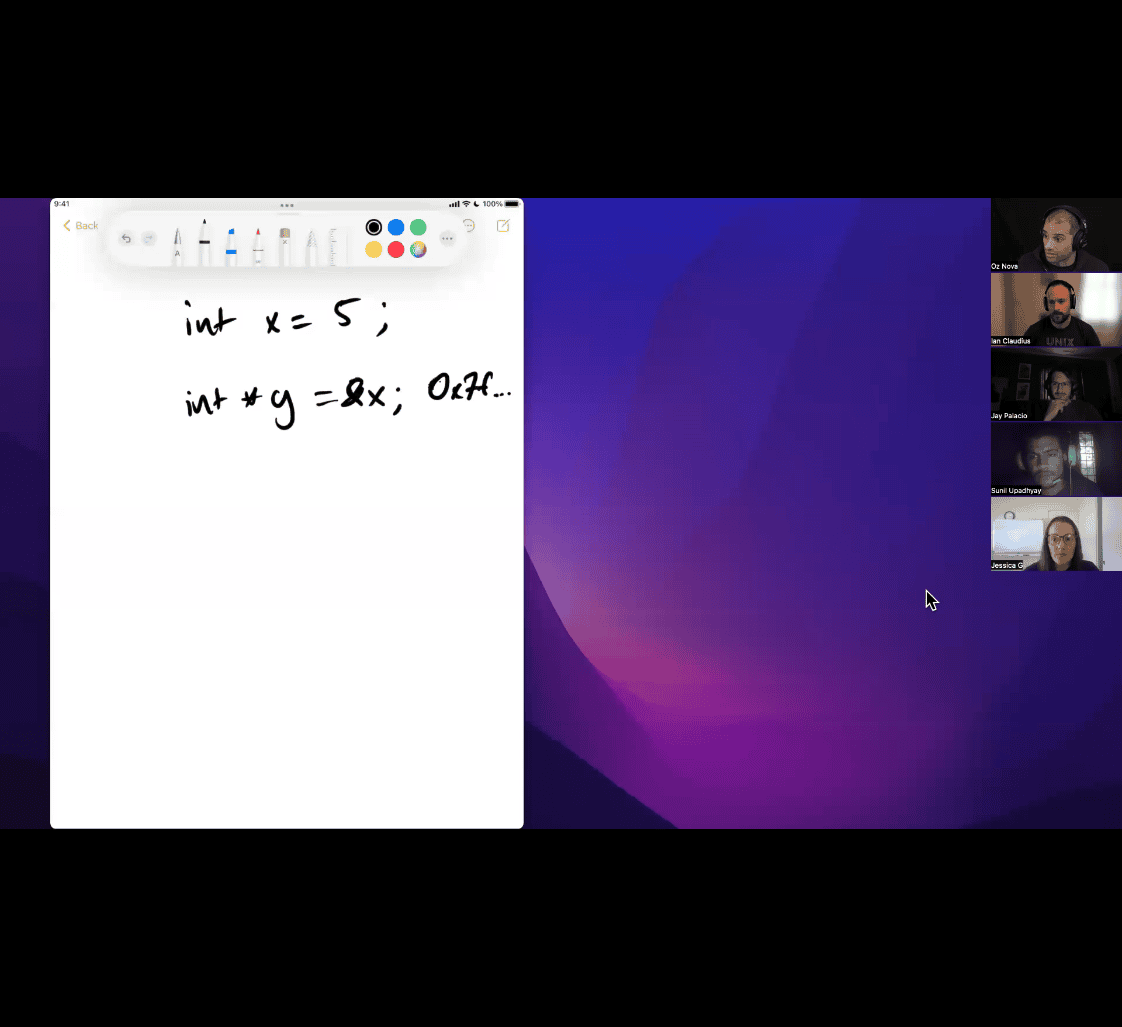 y:
y:
- 64 bits values →
int **z = &y; OR &(&x); → same (type decoration) (two derefercing)
int d = **z; ? asking
int e = **(&&x);
adding 1 to a adderss → get you another address(refercen to a int), adding 1 to a int → get the number
- one is 64bits , another is 32bits
beware of the type mismatch,
Let’s break it down in clear steps:
🧠 1. int x = 5; → What happens?
When you declare:
int x = 5;You are:
- Creating a variable
x - Storing the value
5in it - The value
5is of typeint, which is typically 32 bits (4 bytes) on modern systems (even 64-bit ones)
✅ So:
The value of x is 5 → int → 32 bits
📦 2. What about &x (the address of x)?
When you write:
int *y = &x;You’re saying:
- “Let me store the address of
xin a pointery” - This address (like
0x7ffeefbff4ac) is a memory location - On a 64-bit system, addresses are 64 bits (8 bytes)
✅ So:
The address of x is a 64-bit value
The pointer y is also a 64-bit variable (it holds a memory address)
🧠 3. Visualizing x, y, and z
int x = 5; // x = 5
int *y = &x; // y = address of x
int **z = &y; // z = address of yNow, let’s walk through this:
| Variable | Type | Value | Size |
|---|---|---|---|
x | int | 5 | 32 bits |
y | int * | address of x | 64 bits |
z | int** | address of y | 64 bits |
📍 Why This Matters
- Integers like
xare values: 32 bits. - Pointers like
y,zare memory addresses: 64 bits.
The C type system enforces that when you dereference something, you know what type it points to.
*y // means: get the int stored at the address y points to
**z // means: get the int stored at the address that z points to, which itself points to another address (y)🔄 Address Arithmetic Note
You mentioned:
Adding 1 to an address gives you the address of the next value (in that type)
Yes! That’s pointer arithmetic.
For example:
int *p = &x;
p + 1 // moves forward by 4 bytes (size of int)Because p is an int*, p + 1 means “skip one int” = +4 bytes.
If it were a double*, p + 1 would mean +8 bytes (size of double).
✅ TL;DR
| Concept | Explanation |
|---|---|
int x = 5; | Stores a 32-bit value (on most systems) |
&x | Gives you the 64-bit memory address of x |
int *y = &x; | Pointer y stores a 64-bit address |
int **z = &y; | Pointer-to-pointer z stores y’s address |
So:
- Value (
x) = 32 bits - Address of x (
&x) = 64 bits on 64-bit systems
This distinction between value and address is fundamental in C.
void pointer +1 will get you very next address
“Void pointer +1 will get you very next address, generic pointer”
This is a deep concept in C involving void* (a generic pointer), and how pointer arithmetic works.
🔍 What is a void*?
In C:
void *p;This is a generic pointer — it can point to any type, but the compiler doesn’t know the size of the thing it’s pointing to.
For example:
int x = 5;
void *p = &x; // ok: p points to an int, but compiler doesn't know that✅ void* is often used in:
- Memory functions like
malloc - Data structures like linked lists
- APIs that work with many types
❌ Pointer Arithmetic Is Not Allowed on void* (in C)
Your teacher said:
“void pointer + 1 will get you very next address”
That’s only partially true, and it depends on the language:
🛑 In C
void *p = malloc(10);
p = p + 1; // ❌ Error: arithmetic on a pointer to void is not allowed- Why? Because C doesn’t know the size of a
void, so it can’t calculatep + 1 - You need to cast the pointer first:
p = (char *)p + 1; // ✅ now it works — moves 1 byte forward✅ In GNU C extensions or C++, some compilers may allow it
p + 1is treated like adding 1 byte- This is non-standard, but that’s what your teacher might mean when they say “get next address”
🧠 Why Cast to char* or uint8_t*?
If you want to move byte-by-byte:
void *p = malloc(100);
char *cp = (char *)p;
cp = cp + 1; // ✅ move 1 byteOr:
uint8_t *bp = (uint8_t *)p;
bp += 5; // move 5 bytes✅ Summary
| Concept | Explanation |
|---|---|
void* | Generic pointer to unknown type |
Cannot do void* + 1 in C | Compiler doesn’t know the size of the pointed-to type |
Cast to char* to do math | Moves 1 byte at a time |
p + 1 after cast | Advances 1 byte (for char*), 4 bytes for int*, etc. |
| Your teacher’s point | Adding 1 to a casted void* gives you the next memory address, byte by byte |
👀 Example Demo
#include <stdio.h>
#include <stdlib.h>
int main() {
void *p = malloc(10);
printf("Original: %p\n", p);
// Cast to char* to do arithmetic
void *q = (char *)p + 1;
printf("After +1: %p\n", q);
free(p);
return 0;
}This will print two addresses, 1 byte apart.
Absolutely! Casting is a core concept in C, and it’s essential for low-level control and understanding how C manages memory and types.
🔁 What Is a Cast?
Casting in C means explicitly converting a value from one type to another.
You do this using this syntax:
(new_type) value✅ Example 1: Simple cast (numeric)
int a = 10;
int b = 3;
float result = (float)a / b;a / bwould normally do integer division:10 / 3 = 3- But
(float)aconvertsato 10.0 - So
(float)a / bbecomes10.0 / 3=3.333...
👉 Why cast here? To get floating point division.
🧠 Two Main Kinds of Casts
1. ✅ Value casts (like int → float, or char → int)
Used for arithmetic or formatting:
int a = 65;
char c = (char)a; // c now holds 'A'2. 🔧 Pointer casts (like void* → int*, or char* → void*)
Used when working with memory:
void *p = malloc(sizeof(int));
int *ip = (int *)p; // now you can dereference it like an int*👉 You tell the compiler:
“Hey, trust me — this memory is actually of type
int*.”
⚠️ Why Casts Are Powerful (and Dangerous)
C gives you low-level control, but you must be careful.
Example: memory reinterpretation
float pi = 3.14;
int *hack = (int *)π
printf("%x\n", *hack); // view raw bits of float as an int- Here, you’re reinterpreting the memory of
pias if it’s anint - Useful in systems, hardware, and networking — but dangerous if misused
🧰 Common Use Cases
| Use Case | Example |
|---|---|
| Prevent integer division | (float)a / b |
| Pointer type conversion | (int *)void_ptr |
| Byte-wise memory access | (char *)array + i |
| Type punning / bit manipulation | (int *)&float_var |
Casting away const (rare) | (int *) (uintptr_t) const_ptr |
👎 What You Should Not Do
Example: invalid pointer cast
float pi = 3.14;
int *ip = (int *)π // not safe: breaks strict aliasingThis may work on your machine, but it’s undefined behavior in C.
✅ Safer way: use memcpy() to extract raw bytes.
🧠 Cast vs Implicit Conversion
C sometimes auto-converts types, like:
int x = 10;
float y = x; // auto-cast to floatBut you cast manually when:
- You need precision
- You deal with raw memory or void pointers
- You want to override default behavior
🎯 TL;DR Summary
| Concept | Explanation |
|---|---|
| Cast | Explicitly convert a value to another type |
| Syntax | (new_type) value |
| Why | Fix type mismatches, enable memory tricks, control behavior |
| Risks | You bypass type safety — can cause bugs or crashes |
Would you like a visual diagram of how pointer casting affects memory interpretation?
pointer attacking → make it larger bits

Great question — your teacher is definitely trying to explain a concept that trips up a lot of learners: pointers to pointers (especially void ** or int **) and how function parameters work when you’re modifying data through multiple layers of indirection.
🧠 WHAT IS HE TEACHING?
Your teacher is teaching pointer-to-pointer logic, likely in the context of:
- Passing an array of pointers (e.g.,
char *argv[]orint *p[]) - Dynamic memory allocation
- Understanding why you need
T **when you want to modify a pointer itself inside a function
🔍 Image Context Breakdown
Let’s interpret the image step by step:
Top
int ** → sum_of_n((int **)int1)
- Looks like a function is accepting an
int **parameter. - He may be simulating the signature:
int sum_of_n(int **arr)(orint sum_of_n(int *arr[])) - The
(int **)int1indicates a cast, forcing something to be treated as anint**.
Bottom
q → p1 → 3
p2 → 5
p3 → 6
Looks like:
int a = 3, b = 5, c = 6;
int *p1 = &a;
int *p2 = &b;
int *p3 = &c;
int *arr[] = {p1, p2, p3};
int **q = arr; // q points to p1So q is int **, pointing to an array of int *.
🎯 What is p1, and Why is q a Pointer-to-Pointer?
🧩 The key logic
p1isint *→ it holds the address of anint(like&a)arris an array ofint *→ e.g.,{p1, p2, p3}qis a pointer to the array — so its type isint **
Because
qpoints top1, andp1points to3,qis two levels of indirection away from3.
So:
**q == *p1 == 3💡 Why is this confusing to many?
Because it’s easy to mix up:
| Expression | Meaning | Type |
|---|---|---|
x | variable (e.g., int x) | int |
&x | address of x | int * |
*p | dereference once | int |
**q | dereference twice | int |
q | pointer to pointer | int ** |
✅ Summary
p1is of typeint *qis of typeint **— a pointer top1- You need a
**(pointer to pointer) when you want to pass a pointer by reference (like changing what a pointer points to) - This is a common source of bugs/confusion, especially when doing dynamic allocation or pointer array manipulation
🔧 Real-world example: Allocating memory
void make_array(int **p) {
*p = malloc(sizeof(int) * 10); // modify the original pointer
}This works because you’re passing an int ** — a pointer to the original pointer. Inside the function, *p = ... updates the actual pointer that the caller sees.
**
qis avoid **(pointer to a void pointer)**
This is a classic topic in generic programming and memory manipulation in C, and it’s very useful to understand **how and why you’d use void **instead ofint **orchar ****.
🧠 What Is void **?
void *→ a generic pointer, it can point to any data type (e.g.,int,float,char, etc.)void **→ a pointer to avoid *, or in simpler terms: a reference to a generic pointer
This means:
void *p→ holds the address of some datavoid **q = &p→ holds the address of the pointerp
✅ Real Use Case: Generic Memory Setters
Imagine a function like:
void set_pointer(void **target, void *value) {
*target = value;
}You can call it like this:
int x = 5;
void *p = NULL;
set_pointer(&p, &x);
// now p points to xThis is generic, because you’re not tied to int ** or char ** — you’re using void ** to work with **any pointer-to-pointer** setup.
🧩 Applying to Your Teacher’s Diagram
Let’s say your teacher has something like this:
int a = 3, b = 5, c = 6;
int *p1 = &a;
int *p2 = &b;
int *p3 = &c;
void *arr[] = {p1, p2, p3}; // array of void* pointers (generic pointers)
void **q = arr; // pointer to a void pointerarris of typevoid *[3]→ array of generic pointersqisvoid **→ can be used to access and manipulate any of those pointers
So:
(int *)q[0] → is same as (int *)p1 → points to a
*(int *)q[0] → dereferences to value of a (3)🚨 Why Is This Confusing?
Because with void *, you can’t dereference directly — the compiler doesn’t know what data size/type it’s pointing to.
You always need to cast before dereferencing:
*(int *)q[0] // cast void * to int *, then dereferenceThat’s what your teacher is likely trying to highlight.
🧠 What’s the Takeaway?
-
void **lets you pass a pointer to any pointer (generic and flexible) -
It’s used when you need to:
- Pass a pointer and allow the function to modify it
- Work with multiple pointer types generically (e.g., in
qsort, callbacks, allocators)
-
You must cast when dereferencing
void *orvoid **to access the actual value
Would you like a visual explanation of void *, void **, and how dereferencing works step by step in memory?
You’re doing a dynamic array in C, and your teacher is saying:
❗️”Change
void* arr;tovoid** arr;”
Let’s break this down step by step and learn why.
🧠 Part 1: What Does void* arr; Mean?
This means arr is a generic pointer, and it can point to:
- an
int*,char*,float*— a single element or the beginning of an array
But void* is just one pointer.
If you write:
void* arr = malloc(10 * sizeof(int));You are allocating space for 10 integers, but:
arris still a single pointer- You must cast it to
(int*)to use it
So arr can point to a block of memory holding ints, chars, etc.
🔁 Now What If You Use void** arr;?
Now arr is a pointer to a pointer, which means:
- You can store multiple pointers inside (like a table of pointers)
- Useful for things like:
- dynamic arrays of strings
- dynamic arrays of pointers to structs
- generic containers
For example:
void** arr = malloc(10 * sizeof(void*));
arr[0] = malloc(sizeof(int)); // first element
arr[1] = malloc(sizeof(float)); // second elementYou can store anything in each slot, but:
- each
arr[i]is avoid*pointing to data arritself is avoid**pointing to thosevoid*s
✅ Your Case: Dynamic Array (Generic)
If you want a dynamic array of values like int[], then void* arr is fine, because it’s one block of memory:
void* arr = malloc(N * sizeof(int));But if your goal is to store pointers to things (e.g., int*, char*, struct*), then you need:
void** arr = malloc(N * sizeof(void*));📦 Example Use Case
void* arr (raw block of memory)
typedef struct {
int size;
void* arr;
} DA;
DA* da = malloc(sizeof(DA));
da->arr = malloc(10 * sizeof(int)); // raw data buffer
((int*)da->arr)[0] = 42; // cast to accessvoid** arr (array of pointers)
typedef struct {
int size;
void** arr;
} DA;
DA* da = malloc(sizeof(DA));
da->arr = malloc(10 * sizeof(void*)); // array of generic pointers
da->arr[0] = malloc(sizeof(int)); // store pointer to int
*(int*)(da->arr[0]) = 42; // store value through pointerThis version lets each element be its own pointer (could point to strings, structs, etc.)
🔧 So What Is Your Teacher Trying to Do?
Your teacher might want to:
- Make a dynamic array that can store any type of pointer (generic)
- Allow each slot in the array to point to a separate object
- Give students flexibility in working with different data structures
So:
void** arr;Means: “an array of generic pointers”
🔍 Final Analogy
| Type | Meaning | Use Case |
|---|---|---|
int* | pointer to int | single int or int array |
void* | generic pointer to one block | single buffer |
void** | pointer to a pointer (array of ptrs) | dynamic array of any pointers |
Would you like me to build a working code example showing the difference between void* vs void** in a dynamic array?