20250708-csprimer-computersystem-concept4

csprimer-computersystem-concept4

053 What happens in the compilation pipeline

Call → Compile assemble link load

main.c (source) → assemble code → main.o → a.out(binary)

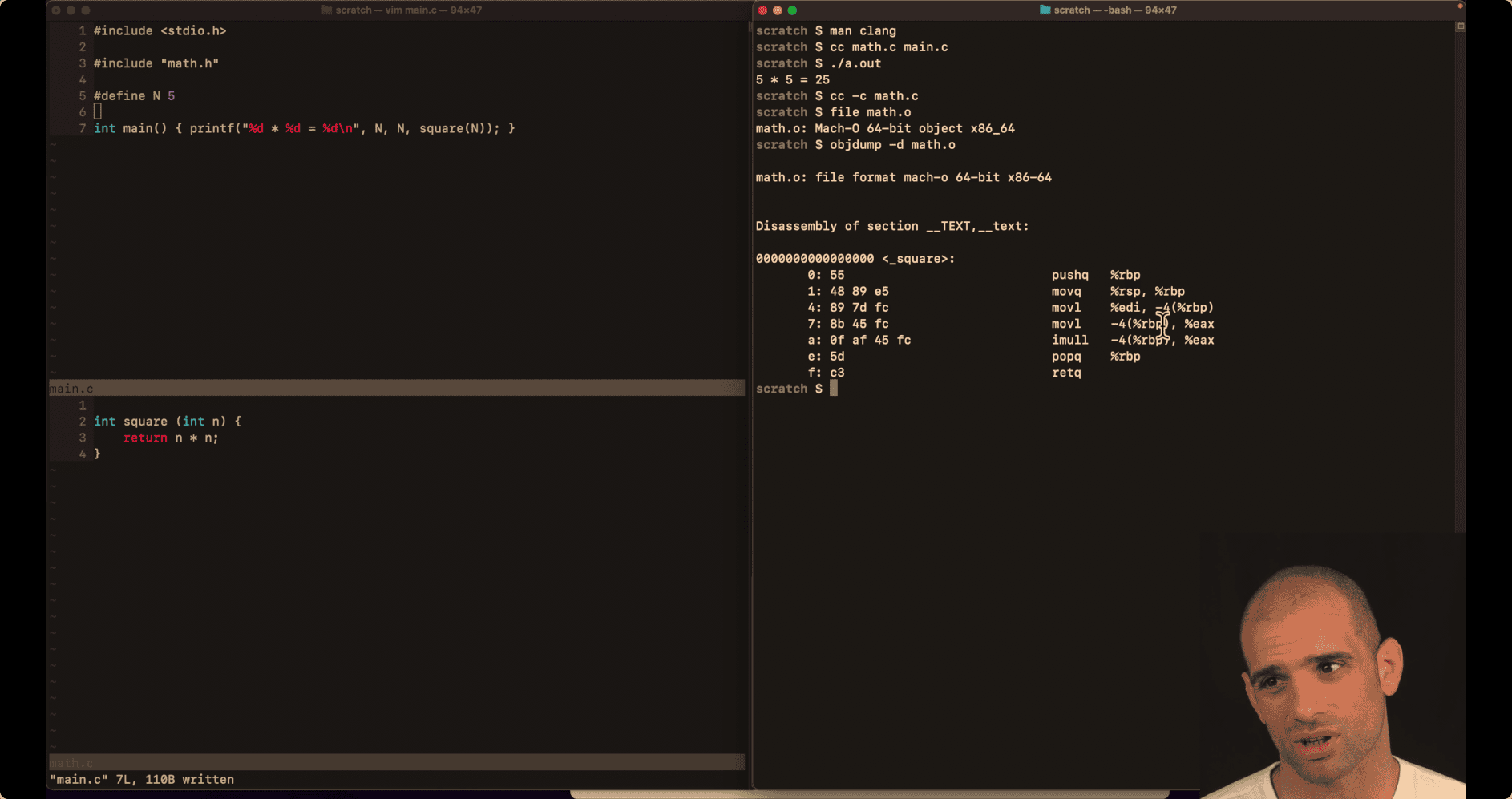
objdump hexdump

cc -c → math.c → obj without link method 1: cc (two .c) ./a.out

method2: cc -c main.c cc main.o math.o ./a.out

man clang → short view of how Complier do, parts

cc -E main.c -E Run the preprocessor stage.

• this is the Preprocessing output

Assembling output: (llvm process)

cc -S main.c -S Run the previous stages as well as LLVM generation and optimization stages and target-specific code generation, cat main.s

---

045 Helping Max rotate bits right

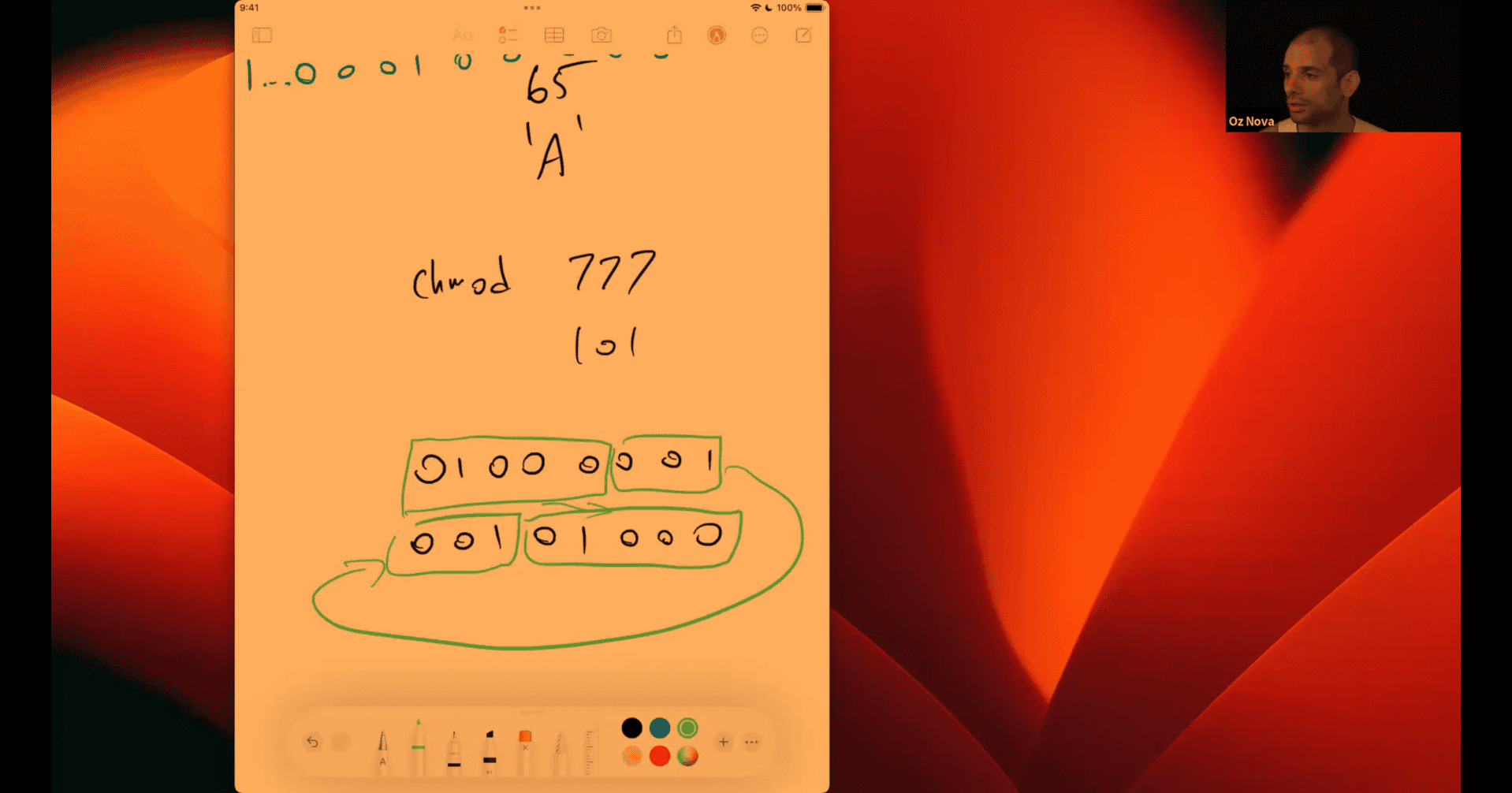unsigned 8 bits

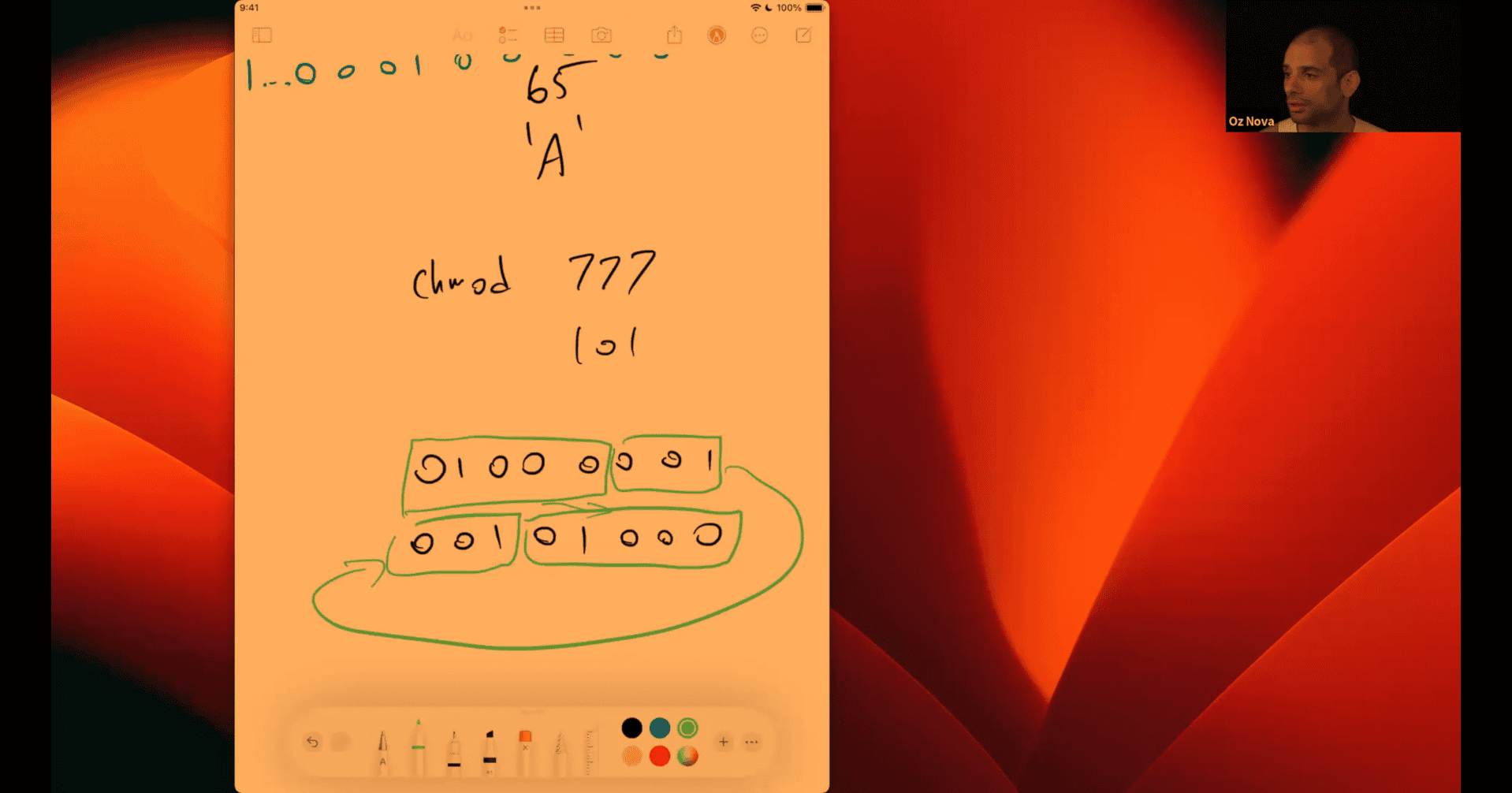copy that part → add or shift 1 and then combine the other part

in node:

-8 >>1 -4 -8 >>>1 (it will give positive number ) 2147483644

if it is signed int, need to use logical right shift

number → first digit bit → second digit

cpu : arithmetical shift or logical shift

---

extra ai finding % and & (out topic)

Let’s use k = 19 and n = 8:

• 19 in binary: 00010011
• 8 in binary: 00001000
• n - 1 = 7 in binary: 00000111

Bitwise operation:

   00010011   (19)
&  00000111   (7)
------------
   00000011   (3)

So, 19 & 7 = 3

Math operation:

19 % 8 = 3

Result:
Both 19 % 8 and 19 & 7 give 3, because & 7 keeps only the last 3 bits, which is the remainder when dividing by 8.

only when k is a power of 2 (like 2, 4, 8, 16, etc.) can you use x & (k - 1) instead of x % k.

For other values of k, this does not work.
Example:

• For x = 7, k = 5:
  • 7 % 5 = 2
  • 7 & 4 = 4 (wrong result)
    So, use x & (k - 1) only when k is a power of 2.

---

• some bit review: Original n: 101100
  n - 1: 101011
  n & (n - 1): 101000

Step-by-step:

• The rightmost 1 in 101100 is at position 2 (from the right).
• Subtracting 1 flips that 1 to 0 and all trailing 0s to 1s: 101011.
• ANDing:
  101100
  & 101011
  = 101000

n & (n - 1):Result: The rightmost 1 is cleared.

n & 1 checks if the rightmost bit of n is 1 (odd) or 0 (even).

Example:
n = 6 (binary: 110)
n & 1 = 110 & 001 = 000 → result is 0 (even)

n = 7 (binary: 111)
n & 1 = 111 & 001 = 001 → result is 1 (odd)

So, n & 1 extracts the least significant bit.

Method	Iterations Needed	Performance Benefit
n >>= 1 >> =	Up to 32	Slower for sparse bits
n &= (n-1)	Only set bits (Hamming weight)	Faster overall

---

bool ispangram(char *s) {
  uint32_t bs = 0;
  char c;
  while (*s != '\n') {
    /* c = tolower(*s); */
    /* s++; */
    c = tolower(*s++);
    if (c < 'a' || c > 'z')
      continue;
    bs |= 1 << (c - 'a');
  }
  // TODO implement this!
  return bs == 0x03ffffff; // how is  this 26 bits are set
//So, `return bs == 0x03ffffff;` returns true only if all 26 letters were found.
}
 

bs (binary): 00000000000000000000000000
              ^                        ^
             'a'                     'z'

Suppose the string is “bad”:

1. Start: bs = 00000000000000000000000000

2. For ‘b’:

   • ‘b’ - ‘a’ = 1
   • Set bit 1:
     bs = 00000000000000000000000010

3. For ‘a’:

   • ‘a’ - ‘a’ = 0
   • Set bit 0:
     bs = 00000000000000000000000011

4. For ‘d’:

   • ‘d’ - ‘a’ = 3
   • Set bit 3:
     bs = 00000000000000000000001011

Visual:
Each time a letter is found, its corresponding bit is turned ON (set to 1).
So, after “bad”, bits for ‘a’, ‘b’, and ‘d’ are set:

bs (binary): 00000000000000000000001011
              zyxwvutsrqponmlkjihgfedcba

Read from right to left:

• The rightmost bit is ‘a’, next is ‘b’, then ‘c’, etc.
• After “bad”, bits for ‘a’, ‘b’, and ‘d’ are 1.

---

Key Differences Between the Two Pangram Implementations

Both use bit manipulation, but there are important differences in approach and efficiency:

---

🔍 Character Processing

Your Version:

c = tolower(*s++);
if (c < 'a' || c > 'z')
    continue;
bs |= 1 << (c - 'a');

Vim Version:

while ((c = *s++) != '\0') {
    if (c < '@') continue; // ignore first 64 chars
    bs |= 1 << (c & 0x1f);
}

Differences:

• Your version: Uses tolower() function call + explicit range check
• Vim version: Uses bitwise AND (& 0x1f) + simpler range check
• Vim version is faster: No function call overhead

---

🎯 Bit Mapping

Your Version:

bs |= 1 << (c - 'a');  // 'a' maps to bit 0, 'z' maps to bit 25

Vim Version:

bs |= 1 << (c & 0x1f);  // 'a'/'A' maps to bit 1, 'z'/'Z' maps to bit 26

Key Insight:

• Your version: 'a' - 'a' = 0, so ‘a’ uses bit 0
• Vim version: 'a' & 0x1f = 97 & 31 = 1, so ‘a’ uses bit 1
• Vim version: 'A' & 0x1f = 65 & 31 = 1, so ‘A’ also uses bit 1

---

🔢 Mask Comparison

Your Version:

return bs == 0x03ffffff;  // 26 bits set: 00000011 11111111 11111111 11111111

Vim Version:

return (bs & MASK) == MASK;  // MASK = 0x07fffffe: 00000111 11111111 11111111 11111110

Bit Analysis:

• Your mask: 0x03ffffff = bits 0-25 set (26 bits total)
• Vim mask: 0x07fffffe = bits 1-26 set (26 bits total)

---

⚡ Performance Comparison

Aspect	Your Version	Vim Version
Case handling	tolower() function call	Bitwise AND (faster)
Range check	c < 'a' || c > 'z'	c < '@' (simpler)
Bit calculation	c - 'a' (subtraction)	c & 0x1f (bitwise AND)
Bit positions	0-25	1-26

Vim version advantages:

• No function calls (tolower() is expensive)
• Simpler range checking
• More efficient bit operations
• Case-insensitive without function calls

---

🎯 Why Vim Version is More Efficient

1. tolower() vs & 0x1f:

   // Your version: function call overhead
   c = tolower(*s++);
    
   // Vim version: direct bit manipulation
   c = *s++;  // no function call

2. Range checking:

   // Your version: two comparisons
   if (c < 'a' || c > 'z')
    
   // Vim version: one comparison
   if (c < '@')

3. Bit mapping:

   // Your version: arithmetic
   c - 'a'  // requires subtraction
    
   // Vim version: bitwise
   c & 0x1f  // faster bitwise operation

---

�� Both Work, But Vim Version is Optimized

Both implementations correctly detect pangrams, but the vim version uses more efficient bit manipulation techniques to achieve the same result with better performance. The key insight is using & 0x1f to handle case-insensitive letter mapping without function calls.

---

continue:

Understanding the Vim Version Bitwise Operation

Let me break down the magic of c & 0x1f with concrete examples!

---

🎯 The Core Trick: c & 0x1f

What 0x1f means:

• 0x1f = 31 in decimal = 00011111 in binary
• It’s a mask that keeps only the last 5 bits

Why 5 bits?

• We need to represent 26 letters (a-z)
• 2⁵ = 32, so 5 bits can represent 0-31
• Perfect for our 26 letters!

---

📊 Bit-by-Bit Examples

Example 1: Letter ‘a’ (lowercase)

'a' = 97 decimal = 01100001 binary
0x1f = 31 decimal = 00011111 binary

'a' & 0x1f:
  01100001  (97)
& 00011111  (31)
= 00000001  (1)

So 'a' maps to bit position 1

Example 2: Letter ‘A’ (uppercase)

'A' = 65 decimal = 01000001 binary
0x1f = 31 decimal = 00011111 binary

'A' & 0x1f:
  01000001  (65)
& 00011111  (31)
= 00000001  (1)

So 'A' also maps to bit position 1!

Example 3: Letter ‘z’ (lowercase)

'z' = 122 decimal = 01111010 binary
0x1f = 31 decimal = 00011111 binary

'z' & 0x1f:
  01111010  (122)
& 00011111  (31)
= 00011010  (26)

So 'z' maps to bit position 26

---

🔍 Complete Letter Mapping

Letter	ASCII	Binary	& 0x1f	Bit Position
’a’/‘A’	97/65	01100001/01000001	1	Bit 1
’b’/‘B’	98/66	01100010/01000010	2	Bit 2
’c’/‘C’	99/67	01100011/01000011	3	Bit 3
…	…	…	…	…
‘z’/‘Z’	122/90	01111010/01011010	26	Bit 26

---

🎯 Why This Works for Case-Insensitive

The Magic:

• Uppercase ‘A’ = 65 = 01000001
• Lowercase ‘a’ = 97 = 01100001
• Both have the same last 5 bits: 00001
• & 0x1f extracts only those last 5 bits!

Visual Comparison:

'A': 01000001
'a': 01100001
     ^^^^^^^^
     Last 5 bits are identical!

---

🔧 Step-by-Step Process

For input: “Hello”

1. ‘H’ (72):

   72 & 0x1f = 01001000 & 00011111 = 00001000 = 8
   Set bit 8: bs |= 1 << 8
   

2. ‘e’ (101):

   101 & 0x1f = 01100101 & 00011111 = 00000101 = 5
   Set bit 5: bs |= 1 << 5
   

3. ‘l’ (108):

   108 & 0x1f = 01101100 & 00011111 = 00001100 = 12
   Set bit 12: bs |= 1 << 12
   

4. ‘l’ (108): (same as above, bit already set)

5. ‘o’ (111):

   111 & 0x1f = 01101111 & 00011111 = 00001111 = 15
   Set bit 15: bs |= 1 << 15
   

Result: bs has bits 5, 8, 12, and 15 set.

---

🎯 The Final Check

Mask: 0x07fffffe

0x07fffffe = 00000111 11111111 11111111 11111110
             ^^^^^^^^  ^^^^^^^^^^^^^^^^^^^^^^^^^^^
             Bits 1-26 set (26 bits total)

Check: (bs & MASK) == MASK

• If all 26 letters are found, bs will have bits 1-26 set
• bs & MASK extracts only bits 1-26
• If it equals MASK, all 26 letters were found!

---

🎯 Why This is Better Than tolower()

Your approach:

c = tolower(*s++);  // Function call overhead
if (c < 'a' || c > 'z') continue;  // Two comparisons
bs |= 1 << (c - 'a');  // Subtraction

Vim approach:

c = *s++;  // No function call
if (c < '@') continue;  // One comparison
bs |= 1 << (c & 0x1f);  // Bitwise AND (faster than subtraction)

The bitwise approach eliminates function calls and uses faster operations!

---

void DA_push(DA *da, void *x) {
  da->items[da->length++] = x;
  // TODO push to the end
  /* `da->items[da->length++] = x;` works as follows: */
  /**/
  /* - `da->length` is the current number of items in the array. */
  /* - `da->items[da->length]` points to the next empty slot (right after the
   * last item). */
  /* - `= x` assigns `x` to that slot. */
  /* - `da->length++` increases the length by 1, so the next push will go to the
   * next slot. */
  /**/
  /* This way, each new item is placed at the end of the array. */
}
 

---

dynamic array:

Looking at the selected line and the context, void **items is a double pointer (pointer to pointer). Here’s why this design is used:

Why void **items (double pointer)?

1. Generic storage: void * can point to any data type, making the array generic
2. Array of pointers: void ** is an array of void * pointers
3. Dynamic allocation: Each element is a pointer to data stored elsewhere

Memory layout:

DA struct:
┌─────────────┐
│ void **items│ ──┐
│ int length  │   │
│ int capacity│   │
└─────────────┘   │
                  │
                  ▼
Array of pointers: [void*][void*][void*][void*]...
                     │     │     │     │
                     ▼     ▼     ▼     ▼
                   data   data  data  data

Why not just void *items?

• void *items would be a single pointer to one piece of data
• void **items is a pointer to an array of pointers, allowing multiple elements

In your code:

// Allocates array of STARTING_CAPACITY pointers
da->items = malloc(STARTING_CAPACITY * sizeof(void *));
 
// Each element stores a pointer to actual data
da->items[da->length++] = x;  // x is a pointer (like &x, &y)

This allows storing pointers to different data types (&x for int, &y for float) in the same dynamic array.

---

Excellent question! You’re confusing two different concepts. Let me clarify:

--da->length vs --pointer

What --da->length Actually Does

--da->length is pre-decrementing an INTEGER, not a pointer!

• da->length is an int (the count of items)
• --da->length decrements this integer by 1
• This has nothing to do with pointer arithmetic

Visual Example

// Before pop: da->length = 3
// Array: [item0, item1, item2, empty, ...]
//         index 0    1     2      3
//                          ↑
//                    last valid item at index 2
 
void *DA_pop(DA *da) {
    return da->items[--da->length];
}
 
// What happens:
// 1. --da->length: decrements length from 3 to 2
// 2. da->items[2]: access the item at index 2 (the last item)
// 3. Return that item
 
// After pop: da->length = 2
// Array: [item0, item1, ???, empty, ...]
//         index 0    1     2     3
//                          ↑
//                    no longer part of array

Why Pre-decrement (--) Instead of Post-decrement (--)?

In DA_pop(), we need pre-decrement because:

// Before: length = 3, last item is at index 2
// Array indices: [0, 1, 2] - but length is 3
 
return da->items[--da->length];
// 1. First: decrement length from 3 to 2
// 2. Then: use the new value (2) as index
// 3. Return da->items[2] - which is the last item!

If we used post-decrement (wrong):

return da->items[da->length--];  // WRONG!
// 1. First: use current length (3) as index
// 2. Then: decrement length to 2
// 3. Return da->items[3] - which is OUT OF BOUNDS!

Pointer Arithmetic vs Integer Arithmetic

You’re thinking of pointer arithmetic:

int *ptr = &array[5];
ptr--;  // Now points to array[4] (previous memory address)

But da->length is just an integer counter:

int length = 5;
--length;  // Now length = 4 (just a number, not an address)

The Pattern

• DA_push(): da->items[da->length++] - use current length, then increment
• DA_pop(): da->items[--da->length] - decrement first, then use new value

Both ensure da->length always represents the count of valid items!

---

#include <assert.h>
#include <stdio.h>
#include <stdlib.h>
 
#define STARTING_CAPACITY 8
 
typedef struct DA {
  void **items; // pointer to anything
  int length;   // number of items
  int capacity;
  // TODO define our struct
} DA;
 
// Helper function to expand the array when it gets full
void DA_expand(DA *da) {
  // Double the capacity (common strategy)
  int new_capacity = da->capacity * 2; //  or use capacity <<= 1;
 
  // Allocate new, larger array
  void **new_items = realloc(da->items, new_capacity * sizeof(void *));
 
  // Check if allocation succeeded
  if (new_items == NULL) {
    printf("Error: Failed to expand dynamic array!\n");
    exit(1);
  }
 
  // Update the DA structure
  da->items = new_items;
  da->capacity = new_capacity;
}
 
DA *DA_new(void) {
  DA *da = malloc(sizeof(DA));      // Allocate memory for the DA struct
  da->length = 0;                   // Start with 0 items
  da->capacity = STARTING_CAPACITY; // Set initial capacity
  da->items =
      malloc(STARTING_CAPACITY * sizeof(void *)); // Allocate array of pointers
  return da;
  //- `DA *da` declares a pointer variable named `da` of type `DA`.
}
 
int DA_size(DA *da) {
  return da->length;
  // TODO return the number of items in the dynamic array
}
 
void DA_push(DA *da, void *x) {
  // Check if we need to expand the array
  if (da->length >= da->capacity) {
    DA_expand(da);
  }
 
  // Add the item at the end
  da->items[da->length] = x;
  da->length++;
 
  // TODO push to the end
  /* `da->items[da->length++] = x;` works as follows: */
  /**/
  /* - `da->length` is the current number of items in the array. */
  /* - `da->items[da->length]` points to the next empty slot (right after the
   * last item). */
  /* - `= x` assigns `x` to that slot. */
  /* - `da->length++` increases the length by 1, so the next push will go to the
   * next slot. */
  /**/
  /* This way, each new item is placed at the end of the array. */
}
 
void *DA_pop(DA *da) {
  // Check if array is empty
  if (da->length <= 0) {
    return NULL;
  }
 
  // Decrement length and return the last item
  da->length--;
  return da->items[da->length];
  // TODO pop from the end
}
 
void DA_set(DA *da, void *x, int i) {
  // Check if index is valid
  if (i < 0 || i >= da->length) {
    return; // Invalid index, do nothing
  }
 
  // Set the value at index i
  da->items[i] = x;
  // TODO set at a given index, if possible
}
 
void *DA_get(DA *da, int i) {
  // Check if index is valid
  if (i < 0 || i >= da->length) {
    return NULL; // Invalid index, return NULL
  }
 
  // Return the value at index i
  return da->items[i];
  // TODO get from a given index, if possible
}
 
void DA_free(DA *da) {
  // TODO deallocate anything on the heap
  free(da->items);
  /* No, only the memory for the `items` array (the pointers) is freed, not the
   * values those pointers reference. */
  free(da);
}
 
int main() {
  DA *da = DA_new();
 
  assert(DA_size(da) == 0);
 
  // basic push and pop test
  int x = 5;
  float y = 12.4;
  DA_push(da, &x);
  DA_push(da, &y);
  assert(DA_size(da) == 2);
 
  assert(DA_pop(da) == &y);
  assert(DA_size(da) == 1);
 
  assert(DA_pop(da) == &x);
  assert(DA_size(da) == 0);
  assert(DA_pop(da) == NULL);
 
  // basic set/get test
  DA_push(da, &x);
  DA_set(da, &y, 0);
  assert(DA_get(da, 0) == &y);
  DA_pop(da);
  assert(DA_size(da) == 0);
 
  // expansion test
  DA *da2 = DA_new(); // use another DA to show it doesn't get overriden , good
                      // for testing
  DA_push(da2, &x);
  int i, n = 100 * STARTING_CAPACITY, arr[n];
  for (i = 0; i < n; i++) {
    arr[i] = i;
    DA_push(da, &arr[i]);
  }
  assert(DA_size(da) == n);
  for (i = 0; i < n; i++) {
    assert(DA_get(da, i) == &arr[i]);
  }
  for (; n; n--)
    DA_pop(da);
  assert(DA_size(da) == 0);
  assert(DA_pop(da2) == &x); // this will fail if da doesn't expand
 
  DA_free(da);
  DA_free(da2);
  printf("OK\n");
}

• all assert passed

void DA_expand(DA *da) {
  // Double the capacity (common strategy)
  int new_capacity = da->capacity * 2; //  or use capacity <<= 1;
 
  // Allocate new, larger array
  void **new_items = realloc(da->items, new_capacity * sizeof(void *));
 
  // Check if allocation succeeded
  if (new_items == NULL) {
    printf("Error: Failed to expand dynamic array!\n");
    exit(1);
  }
 
  // Update the DA structure
  da->items = new_items;
  da->capacity = new_capacity;
}

• the key is auto expand
• double is not optimal , e.g. python double at first (small amount) , then decrease the ratio latter when getting big
• when using assert testing, create another block of memory for second test

No, you cannot use ++da->length in push. Here’s why:

Current push: da->items[da->length++] = x; (CORRECT)

With post-increment (da->length++):

1. First: Use current da->length as array index
2. Then: Increment da->length by 1

Example: If da->length = 2 (items at indices 0, 1):

• Uses index 2 (the next empty slot)
• Assigns x to da->items[2]
• Then increments da->length to 3
• Result: Item added at correct position

If you used da->items[++da->length] = x; (WRONG)

With pre-increment (++da->length):

1. First: Increment da->length by 1
2. Then: Use the incremented value as array index

Example: If da->length = 2 (items at indices 0, 1):

• Increments da->length to 3 first
• Uses index 3 to assign x
• Assigns x to da->items[3]
• Result: Skips index 2! Creates a gap in the array

Why push and pop use different increment styles

• Push: Needs to use the current length as the next available index, then increment
• Pop: Needs to decrement first to get the last valid index, then use it

The operations are asymmetric by nature:

• Push adds at position length, then updates length
• Pop updates length first, then accesses position length-1

---

• 040 Varint C extension

1. Extending Python with C or C++ — Python 3.13.7 documentation Building a Python C Extension Module – Real Python e.g numpy

python variant review:

part |= (n and 0x80 or 0x00)

This is setting bit 7 (the most significant bit) of the current byte to indicate whether more bytes follow in the varint encoding.

Here’s how it works:

1. n and 0x80 - This is a Python idiom that returns 0x80 if n is truthy (non-zero), otherwise 0
2. or 0x00 - This ensures we get 0x00 if the left side is falsy
3. part |= ... - ORs the result with part to set the continuation bit

The purpose: In varint encoding, each byte uses 7 bits for data and 1 bit (the MSB) as a continuation flag:

• If the continuation bit is 1 (0x80): more bytes follow
• If the continuation bit is 0 (0x00): this is the last byte

So when n > 0 (meaning more bits remain to encode), it sets the continuation bit to 1. When n == 0 (this will be the last byte), it sets the continuation bit to 0.

A cleaner way to write this would be:

part |= 0x80 if n else 0x00

The |= operator is the bitwise OR assignment operator. It performs a bitwise OR operation between the left operand and right operand, then assigns the result back to the left operand.

Basic syntax:

a |= b  # equivalent to: a = a | b

# Let's say part = 0x16 (22 in decimal, 7 bits of data)
part = 0x16   # Binary: 00010110
n = 1         # Truthy, so we use 0x80
mask = 0x80   # Binary: 10000000
 
part |= mask
 
# Step by step:
# part = 00010110  (0x16)
# mask = 10000000  (0x80)
# OR =   10010110  (0x96)
# Result: part = 0x96
 
n = 150  # Binary: 10010110
 
# First iteration:
part = n & 0x7f     # part = 150 & 127 = 22 = 0x16
n >>= 7             # n = 150 >> 7 = 1  
n > 0, so: part |= 0x80  # part = 0x16 | 0x80 = 0x96
# Result: 0x96 (binary: 10010110)
 
# Second iteration:  
part = n & 0x7f     # part = 1 & 127 = 1 = 0x01
n >>= 7             # n = 1 >> 7 = 0
n == 0, so: part |= 0x00  # part = 0x01 | 0x00 = 0x01  
# Result: 0x01 (binary: 00000001)
 
# Final encoding: [0x96, 0x01]

the core concept is just take the first (msb ) as condition sign, is if not 0 , and 0x80, if 0 (= end of that bit process) and turn it 0 (otherwise it will just keep looping) → encoder part

#define PY_SSIZE_T_CLEAN
#include <Python.h>
 
static PyObject *cvarint_encode(PyObject *self, PyObject *args) {
  unsigned long long n;
  int i = 0;
  char part, out[10] = {0}; // Initialize array to zero
  if (!PyArg_ParseTuple(args, "K", &n))
    return NULL;
 
  // Handle zero case explicitly
  if (n == 0) {
    out[i++] = 0x00;
  } else {
    while (n > 0) {
      part = n & 0x7f; // Extract the 7 least significant bits
      n >>= 7;
      if (n > 0) {
        part |= 0x80; // Set continuation bit
      }
      out[i++] = part;
    }
  }
 
  return PyBytes_FromStringAndSize(out, i);
}
 
static PyObject *cvarint_decode(PyObject *self, PyObject *args) {
  const char *varn;
  char b;
  unsigned long long n = 0;
  int i, shamt = 0;
  if (!PyArg_ParseTuple(args, "y", &varn))
    return NULL;
 
  for (i = 0;; i++) {
    b = varn[i];
    if (b == 0)
      break;
    n |= ((unsigned long long)(b & 0x7f) << shamt);
    shamt += 7;
  }
  return PyLong_FromUnsignedLongLong(n);
}
 
static PyMethodDef CVarintMethods[] = {
    {"encode", cvarint_encode, METH_VARARGS, "Encode an integer as varint."},
    {"decode", cvarint_decode, METH_VARARGS,
     "Decode varint bytes to an integer."},
    {NULL, NULL, 0, NULL}};
 
static struct PyModuleDef cvarintmodule = {
    PyModuleDef_HEAD_INIT, "cvarint",
    "A C implementation of protobuf varint encoding", -1, CVarintMethods};
 
PyMODINIT_FUNC PyInit_cvarint(void) { return PyModule_Create(&cvarintmodule); }

python setup.py build_ext --inplace python test.py

import struct
import time
import random
import sys
 
import cvarint
 
 
def encode(n):
    out = []
    while n > 0:
        part = n & 0x7F
        n >>= 7
        part |= n and 0x80 or 0x00
        out.append(part)
    return bytes(out)
 
 
def decode(varn):
    n = 0
    for b in reversed(varn):
        n <<= 7
        n |= b & 0x7F
    return n
 
 
if __name__ == "__main__":
    # Basic cases to ensure encoding is correct
    cases = (
        ("1.uint64", b"\x01"),
        ("150.uint64", b"\x96\x01"),
        ("maxint.uint64", b"\xff\xff\xff\xff\xff\xff\xff\xff\xff\x01"),
    )
    for fname, expectation in cases:
        with open(fname, "rb") as f:
            n = struct.unpack(">Q", f.read())[0]
            assert encode(n) == expectation
            assert decode(encode(n)) == n
            # print(f"Expected {cvarint.decode(cvarint.encode(n))} to be {n}")
            assert cvarint.encode(n) == expectation
            # print(f"expected {expectation}, got {cvarint.encode(n)} for {n}")
            assert cvarint.decode(cvarint.encode(n)) == n
 
    # print("ok")
    # sys.exit(0)
    # Now roundtrip test for speed!
    num_cases = 1000000
    py_time = 0
    c_time = 0
 
    print("Running speed test...")
 
    for _ in range(num_cases):
        n = random.getrandbits(64)
        # time the python
        start = time.process_time_ns()
        res = decode(encode(n))
        end = time.process_time_ns()
        py_time += end - start
        assert n == res
        # time the C
        start = time.process_time_ns()
        res = cvarint.decode(cvarint.encode(n))
        end = time.process_time_ns()
        c_time += end - start
        try:
            assert n == res
        except AssertionError:
            print(f"Failed on {n}: round trip result was {res}")
            break
 
    py_time_sec = float(py_time) / 1000000000
    c_time_sec = float(c_time) / 1000000000
    print(
        f"Executed {num_cases:,} random tests\n\n"
        f"Python:\t{int(py_time / num_cases):>6}ns per case "
        f"({py_time_sec:0.3f}s total)\n"
        f"C:\t{int(c_time / num_cases):>6}ns per case "
        f"({c_time_sec:0.3f}s total)"
    )

---

ai ans:

Looking at your C code, let me explain how both the encode and decode functions work:

C Encode Function (cvarint_encode)

The encode function converts an unsigned 64-bit integer into varint format:

1. Input: Takes an unsigned long long (K format in PyArg_ParseTuple)
2. Process:
   • Zero case: If input is 0, directly stores 0x00
   • Non-zero case: Uses a while loop to process 7 bits at a time:
     • part = n & 0x7f - Extract lower 7 bits
     • n >>= 7 - Shift right by 7 bits for next iteration
     • If more data remains (n > 0), set the continuation bit: part |= 0x80
     • Store the byte in the output array
3. Output: Returns a PyBytes object containing the varint-encoded bytes

C Decode Function (cvarint_decode)

The decode function has a critical bug. Here’s how it currently works:

1. Input: Takes a bytes object (y format)
2. Process:
   • Loops through each byte until it finds a 0x00 byte
   • For each byte: n |= ((unsigned long long)(b & 0x7f) << shamt)
   • Increments shift amount by 7 bits each iteration
3. Bug: It stops when it encounters any 0x00 byte, not when the continuation bit is clear

The Problem

The decode function should stop when it finds a byte WITHOUT the continuation bit (0x80), but instead it stops when it finds a zero byte. This works accidentally in your test because:

• Your Python encode function handles zero specially
• The test cases happen to not expose this bug
• But it will fail on many valid varint sequences jjj

Correct Decode Logic

The decode should be:

  for (i = 0;; i++) {
    b = varn[i];
    n |= ((unsigned long long)(b & 0x7f) << shamt);
    shamt += 7;
    if ((b & 0x80) == 0)  // Stop when continuation bit is NOT set
      break;
  }

The current version stops on zero bytes instead of checking the continuation bit, which is why it might fail on certain inputs where a valid varint byte happens to be 0x00 but isn’t the last byte.

---

I’ll use sequential thinking to break down this C function and explain each concept in simple, professional terms.

C Function Breakdown: cvarint_decode Explained Like a Pro

Let me break down this function line by line, explaining each C concept in simple but professional terms!

Function Signature & Purpose

static PyObject *cvarint_decode(PyObject *self, PyObject *args)

What it does: Converts varint bytes back to a Python integer C Concepts:

• static: Function is only visible in this file (encapsulation)
• PyObject *: Everything in Python C API is a PyObject pointer
• self: The module object (usually NULL for module functions)
• args: Tuple of arguments passed from Python

Variable Declarations

const char *varn;           // Pointer to the input bytes
char b;                     // Current byte being processed
unsigned long long n = 0;   // Result accumulator (64-bit integer)
int i, shamt = 0;          // Loop counter and shift amount

C Concepts Explained:

• const char *: Read-only pointer to character data (the bytes)
• unsigned long long: 64-bit unsigned integer (can hold very large numbers)
• int i, shamt = 0: Multiple variable declaration (C shorthand)

Argument Parsing

if (!PyArg_ParseTuple(args, "y", &varn))
    return NULL;

What it does: Extracts the bytes argument from Python C Concepts:

• PyArg_ParseTuple(): Python C API function to parse arguments
• "y": Format code meaning “bytes object”
• &varn: Address of varn (pass by reference)
• return NULL: Signals error to Python (Python C API convention)

Why important: This is how C functions receive Python data safely

The Main Decoding Loop

for (i = 0;; i++) {
    b = varn[i];
    n |= ((unsigned long long)(b & 0x7f) << shamt);
    shamt += 7;
    if ((b & 0x80) == 0)
        break;
}

Let me break this down step by step:

Step 1: Loop Structure

for (i = 0;; i++)

C Concept: Infinite loop with manual break

• i = 0: Start at index 0
• ;;: No condition (infinite loop)
• i++: Increment after each iteration

Step 2: Get Current Byte

b = varn[i];

What it does: Gets the i-th byte from the input C Concept: Array indexing with pointer arithmetic

Step 3: The Magic Bit Operations

n |= ((unsigned long long)(b & 0x7f) << shamt);

This is the heart of the function! Let me explain each part:

b & 0x7f - Extract Data Bits

• 0x7f = 01111111 in binary
• AND operation keeps only the lower 7 bits
• Purpose: Remove the continuation bit, keep only data

(unsigned long long) - Type Casting

• Converts the result to 64-bit integer
• Purpose: Ensures we have enough bits for shifting

<< shamt - Left Shift

• Shifts bits left by shamt positions
• Purpose: Position the data bits correctly in the result

n |= - Bitwise OR Assignment

• ORs the result with the accumulator
• Purpose: Combines this byte’s data with previous bytes

Step 4: Update Shift Amount

shamt += 7;

What it does: Increases shift amount by 7 for next byte Why: Each byte contributes 7 bits, so next byte needs 7 more positions

Step 5: Check for End

if ((b & 0x80) == 0)
    break;

What it does: Checks if this is the last byte C Concept:

• 0x80 = 10000000 in binary (bit 7)
• b & 0x80: Extracts only bit 7
• == 0: Checks if bit 7 is 0 (no more bytes)

Return Value

return PyLong_FromUnsignedLongLong(n);

What it does: Converts C integer to Python integer C Concept:

• PyLong_FromUnsignedLongLong(): Python C API function
• Creates a Python int object from C unsigned long long

Visual Example: Decoding [0x96, 0x01] → 150

Let me create a demonstration to show exactly how this works:

[2 tools called]

Perfect! Now let me explain the key concepts in simple terms:

Key C Concepts Explained Simply

1. Pointers (const char *varn)

const char *varn;

Simple explanation: A pointer is like a street address that tells you where to find data

• varn points to the first byte of our input data
• const means “don’t change the data” (read-only)
• char means each item is a byte (8 bits)

2. Bitwise AND (&)

b & 0x7f

Simple explanation: AND is like a filter that only lets certain bits through

• 0x7f = 01111111 (keeps only the lower 7 bits)
• Purpose: Remove the continuation bit, keep only data

Visual:

Byte:     10010110
Filter:   01111111
Result:   00010110  (only lower 7 bits kept)

3. Left Shift (<<)

data << shamt

Simple explanation: Shifting left moves bits to higher positions (multiplies by 2^shift)

• 1 << 7 = 1 * 2^7 = 128
• Purpose: Position data bits correctly in the result

Visual:

Before: 00000001
After:  10000000  (shifted left by 7)

4. Bitwise OR (|=)

n |= shifted_data

Simple explanation: OR combines bits from two numbers

• If either bit is 1, result is 1
• Purpose: Add this byte’s data to our accumulator

Visual:

n:       00000000 00010110  (22)
data:    00000000 10000000  (128)
result:  00000000 10010110  (150)

5. Type Casting

(unsigned long long)(b & 0x7f)

Simple explanation: Converting from one type to another

• char (8 bits) → unsigned long long (64 bits)
• Purpose: Ensure we have enough bits for shifting

6. Infinite Loop with Break

for (i = 0;; i++) {
    // ... process byte
    if (condition) break;  // Exit when done
}

Simple explanation: Loop until we find the end condition

• Purpose: Process all bytes until we find the last one

Why This Algorithm Works

The Big Picture:

1. Read each byte from the input
2. Extract 7 data bits (remove continuation bit)
3. Position them correctly using left shift
4. Add them to result using bitwise OR
5. Stop when continuation bit is 0

Why Left Shift by 7?

• Each byte contributes 7 bits of data
• First byte: bits 0-6
• Second byte: bits 7-13
• Third byte: bits 14-20
• And so on…

Why OR to Combine?

• OR is perfect for combining non-overlapping bit patterns
• Each byte’s data goes to different bit positions
• OR combines them without interference

Professional Tips

1. Memory Safety

• const char * prevents accidental modification
• Always check bounds in real applications

2. Performance

• Bit operations are very fast
• No multiplication/division needed
• Direct memory access

3. Portability

• unsigned long long ensures 64-bit support
• Bit operations work the same on all platforms

4. Error Handling

• Check for buffer overflows in production code
• Validate input length

This function is a perfect example of efficient C programming: it uses bit operations to achieve maximum performance while maintaining clarity! 🚀

---

041 Basic hashmap

Copilot (14efae81-a0e7-4193-b89f-f53cffe0f011) ───

Looking at this hashmap implementation, let me explain how the hash bucket selection works with detailed examples.

How hash % h->num_buckets Works

The modulo operation (%) maps any hash value to a valid bucket index within the array bounds.

Example with STARTING_BUCKETS = 8:

STARTING_BUCKETS = 8
// So we have buckets indexed: 0, 1, 2, 3, 4, 5, 6, 7

Hash Examples from your code:

printf("%d\n", djb2("oof")); // Let's say this outputs: 193485
printf("%d\n", djb2("foo")); // Let's say this outputs: 193487  
printf("%d\n", djb2("bar")); // Let's say this outputs: 97299

Bucket Assignment:

// For key "oof":
hash = 193485
bucket_index = 193485 % 8 = 5  // Goes to bucket[5]
 
// For key "foo": 
hash = 193487
bucket_index = 193487 % 8 = 7  // Goes to bucket[7]
 
// For key "bar":
hash = 97299  
bucket_index = 97299 % 8 = 3   // Goes to bucket[3]

What the Selected Lines Do:

/* return h->buckets[hash % h->num_buckets]->value; */  // WRONG - assumes only one node
Node *n = h->buckets[hash % h->num_buckets];           // CORRECT - gets head of chain

The commented line is wrong because it assumes there’s exactly one node at that bucket. But with hash collisions, multiple keys can map to the same bucket, forming a linked list.

Visual Example:

Buckets array (size 8):
[0] -> NULL
[1] -> NULL  
[2] -> NULL
[3] -> Node("bar") -> NULL
[4] -> NULL
[5] -> Node("oof") -> NULL
[6] -> NULL
[7] -> Node("foo") -> NULL

With Collision Example:

If two keys hash to the same bucket:

// Both "key1" and "key2" hash to bucket 3
[3] -> Node("key2") -> Node("key1") -> NULL

That’s why the code needs to traverse the linked list at each bucket to find the correct key-value pair by comparing both the cached hash and the actual key string.

#include <assert.h>
#include <stdint.h>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
 
#define STARTING_BUCKETS 8
#define MAX_KEY_SIZE 32 // todo this constraint
 
typedef uint32_t Hash;
 
typedef struct Node {
  char *key;
  void *value;
  Hash hash; // cache it
  struct Node *next;
} Node;
 
typedef struct Hashmap {
  Node **buckets;
  int num_buckets;
} Hashmap;
 
Hash djb2(const char *s) {
  Hash h = 8351;
  char ch;
  while ((ch = *s++))      // *s++ = next item
    h = (h << 5) + h + ch; // moving form *32 to shift 5 times + h
  return h;
}
 
Hashmap *Hashmap_new() {
  Hashmap *h = malloc(sizeof(Hashmap));
  // array here to be malloc aswell:
  h->buckets = calloc(STARTING_BUCKETS, sizeof(Node));
  h->num_buckets = STARTING_BUCKETS;
  return h;
}
 
void Hashmap_free(Hashmap *h) {
  Node *prior, *n;
  for (int i = 0; i < h->num_buckets; i++) {
    n = h->buckets[i];
    while (n != NULL) {
      prior = n;
      n = n->next;
      free(prior->key);
      free(prior);
    }
  }
  // Todo free all the nodes, long running program need to free even os will
  // handle it
  free(h->buckets);
  free(h);
}
 
void Hashmap_set(Hashmap *h, char *key, void *value) {
  Hash hash = djb2(key);
  int i = hash % h->num_buckets;
  Node *n = h->buckets[i];
  while (n != NULL) {
    if (n->hash == hash && strncmp(key, n->key, MAX_KEY_SIZE) == 0) {
      n->value = value;
      return; // stop
    }
    n = n->next;
  }
  // iterate over linked at hash location , if hash and key match given, replace
  // vaule, if no match found, insert new node at head of linked list
  n = malloc(sizeof(Node));
  /* n->key = key // use strdup otherwise the hash map will break */
  n->key = strdup(key); // use strdup otherwise the hash map will break, can't
                        // just point it to key
  n->value = value;
  n->hash = hash;
  n->next = h->buckets[i];
  h->buckets[i] = n;
}
 
void *Hashmap_get(Hashmap *h, char *key) {
  // iterate over linked list hash location
  //  return val if match, otherwise null
  Hash hash = djb2(key);
  /* return h->buckets[hash % h->num_buckets]->value; */
  Node *n = h->buckets[hash % h->num_buckets];
  while (n != NULL) {
    if (n->hash == hash && strncmp(key, n->key, MAX_KEY_SIZE) == 0) {
      return n->value;
    }
    n = n->next;
  }
  return NULL;
}
 
void Hashmap_delete(Hashmap *h, char *key) {
  Hash hash = djb2(key);
  int i = hash % h->num_buckets;
  Node *piror = NULL, *n = h->buckets[i];
  while (n != NULL) {
    if (n->hash == hash && strncmp(key, n->key, MAX_KEY_SIZE) == 0) {
      if (piror == NULL) {
        h->buckets[i] = NULL;
      } else {
        piror->next = n->next;
      }
      free(n);
      return;
    }
    piror = n;
    /* h->buckets[i] = NULL; // not necessarily */
    n = n->next;
 
    // free that as well, that's why people
    // need garbage collector
  }
}
 
int main() {
  Hashmap *h = Hashmap_new();
  printf("%d\n", djb2("oof"));
  printf("%d\n", djb2("foo"));
  printf("%d\n", djb2("bar"));
 
  // basic get/set functionality
  int a = 5;
  float b = 7.2;
  Hashmap_set(h, "item a", &a);
  Hashmap_set(h, "item b", &b);
  assert(Hashmap_get(h, "item a") == &a);
  assert(Hashmap_get(h, "item b") == &b);
 
  // using the same key should override the previous value
  int c = 20;
  Hashmap_set(h, "item a", &c);
  assert(Hashmap_get(h, "item a") == &c);
 
  // basic delete functionality
  Hashmap_delete(h, "item a");
  assert(Hashmap_get(h, "item a") == NULL);
 
  // handle collisions correctly
  // note: this doesn't necessarily test expansion
  int i, n = STARTING_BUCKETS * 10, ns[n];
  char key[MAX_KEY_SIZE];
  for (i = 0; i < n; i++) {
    ns[i] = i;
    sprintf(key, "item %d", i);
    Hashmap_set(h, key, &ns[i]);
  }
  for (i = 0; i < n; i++) {
    sprintf(key, "item %d", i);
    assert(Hashmap_get(h, key) == &ns[i]);
  }
 
  Hashmap_free(h);
 
  /* stretch goals: */
  /* - expand the underlying array if we start to get a lot of collisions */
  /* - support non-string keys */
  /* - try different hash functions */
  /* - switch from chaining to open addressing */
  /* - use a sophisticated rehashing scheme to avoid clustered collisions */
  /* - implement some features from Python dicts, such as reducing space use,
   */
  /* maintaing key ordering etc. see
   * https://www.youtube.com/watch?v=npw4s1QTmPg
   */
  /* for ideas */
  printf("ok\n");
}

this is the finished code ,

explanation:

Hashmap Implementation: Line-by-Line Explanation

🎯 The Big Picture: What is a Hashmap?

Think of a hashmap like a filing cabinet with numbered drawers:

Drawer 0: [empty]
Drawer 1: [apple] → [cherry]  ← Linked list for collisions
Drawer 2: [empty]
Drawer 3: [banana]
...
Drawer 7: [empty]

• Key: The label on the file (like “apple”)
• Value: The actual file contents
• Hash function: The filing system that tells us which drawer to use
• Buckets: The drawers (numbered 0-7)
• Collision: When two files want the same drawer
• Linked list: Multiple files in the same drawer, chained together

📋 Data Structures Explained

The Node Structure

typedef struct Node {
  char *key;        // The label (string)
  void *value;      // The file contents (any type)
  Hash hash;        // The computed hash (cached for speed)
  struct Node *next; // Pointer to next file in same drawer
} Node;

Line-by-line explanation:

• char *key: Pointer to the key string (like “apple”)
• void *value: Pointer to the actual data (can be any type)
• Hash hash: The computed hash value (cached to avoid recomputation)
• struct Node *next: Pointer to the next node in the chain (for collisions)

The Hashmap Structure

typedef struct Hashmap {
  Node **buckets;   // Array of pointers to Node chains
  int num_buckets;  // Number of drawers (8)
} Hashmap;

Line-by-line explanation:

• Node **buckets: Array of pointers to Node chains (the drawers)
• int num_buckets: Number of buckets/drawers (8 in your case)

🔢 Hash Function: The Filing System

Hash djb2(const char *s) {
  Hash h = 8351;    // Start with a prime number
  char ch;
  while ((ch = *s++))      // Get next character, move pointer
    h = (h << 5) + h + ch; // Multiply by 33, add character
  return h;
}

Line-by-line explanation:

Line 1: Hash h = 8351;

• Start with a prime number (primes give better distribution)
• This is our “seed” value

Line 2: char ch;

• Variable to hold each character as we process it

Line 3: while ((ch = *s++))

• *s++: Get the character at current position, then move pointer to next
• ch = *s++: Assign the character to ch
• while ((ch = *s++)): Continue while ch is not null terminator
• This processes each character in the string

Line 4: h = (h << 5) + h + ch;

• h << 5: Shift h left by 5 bits (multiply by 32)
• (h << 5) + h: This equals h * 33 (32 + 1)
• + ch: Add the ASCII value of the current character
• This creates a hash that depends on all characters

Line 5: return h;

• Return the final hash value

Why this works: Each character affects the final hash, and the prime multiplier helps distribute keys evenly.

🏗️ Creating the Hashmap

Hashmap *Hashmap_new() {
  Hashmap *h = malloc(sizeof(Hashmap));  // Allocate hashmap struct
  h->buckets = calloc(STARTING_BUCKETS, sizeof(Node));  // Allocate bucket array
  h->num_buckets = STARTING_BUCKETS;  // Set number of buckets
  return h;  // Return the new hashmap
}

Line-by-line explanation:

Line 1: Hashmap *h = malloc(sizeof(Hashmap));

• malloc(sizeof(Hashmap)): Allocate memory for one Hashmap struct
• Hashmap *h: Create a pointer to hold the address
• This gives us space for the hashmap structure

Line 2: h->buckets = calloc(STARTING_BUCKETS, sizeof(Node));

• calloc(STARTING_BUCKETS, sizeof(Node)): Allocate array of 8 Node structs
• h->buckets: Point the buckets field to this array
• calloc: Like malloc, but initializes memory to zero
• BUG: Should be sizeof(Node *) not sizeof(Node)

Line 3: h->num_buckets = STARTING_BUCKETS;

• Set the number of buckets to 8
• This tells us how many “drawers” we have

Line 4: return h;

• Return the pointer to our new hashmap

Memory layout after creation:

Hashmap h:
┌─────────────────┐
│ buckets: 0x1000  │  ← Points to bucket array
│ num_buckets: 8   │
└─────────────────┘
         │
         ▼
    buckets array:
    ┌─────────┬─────────┬─────────┬─────────┬─────────┬─────────┬─────────┬─────────┐
    │  NULL   │  NULL   │  NULL   │  NULL   │  NULL   │  NULL   │  NULL   │  NULL   │
    └─────────┴─────────┴─────────┴─────────┴─────────┴─────────┴─────────┴─────────┘

➕ Adding Items: Hashmap_set()

void Hashmap_set(Hashmap *h, char *key, void *value) {
  Hash hash = djb2(key);  // Calculate hash for the key
  int i = hash % h->num_buckets;  // Find which bucket to use
  
  Node *n = h->buckets[i];  // Get first node in that bucket
  while (n != NULL) {  // Search through the chain
    if (n->hash == hash && strncmp(key, n->key, MAX_KEY_SIZE) == 0) {
      n->value = value;  // Update existing key
      return;
    }
    n = n->next;  // Move to next node in chain
  }
  
  // Key not found, create new node
  n = malloc(sizeof(Node));  // Allocate new node
  n->key = strdup(key);  // Copy the key string
  n->value = value;  // Set the value
  n->hash = hash;  // Store the hash
  n->next = h->buckets[i];  // Point to current first node
  h->buckets[i] = n;  // Make this node the new first
}

Line-by-line explanation:

Line 1: Hash hash = djb2(key);

• Calculate the hash for the key
• This tells us which “drawer” to use

Line 2: int i = hash % h->num_buckets;

• hash % h->num_buckets: Get remainder when dividing by 8
• This gives us a bucket index between 0 and 7
• Example: hash 12345 % 8 = 1, so use bucket 1

Line 3: Node *n = h->buckets[i];

• Get the first node in the target bucket
• This might be NULL if the bucket is empty

Lines 4-9: Search for existing key

while (n != NULL) {
  if (n->hash == hash && strncmp(key, n->key, MAX_KEY_SIZE) == 0) {
    n->value = value;  // Found existing key, update value
    return;
  }
  n = n->next;  // Move to next node in chain
}

• while (n != NULL): Continue while we have nodes to check
• n->hash == hash: First check if hashes match (fast)
• strncmp(key, n->key, MAX_KEY_SIZE) == 0: Then check if strings match
• n->value = value: Update the existing value
• n = n->next: Move to next node in the chain

Lines 11-16: Create new node if key not found

n = malloc(sizeof(Node));  // Allocate memory for new node
n->key = strdup(key);  // Copy the key string
n->value = value;  // Set the value
n->hash = hash;  // Store the hash
n->next = h->buckets[i];  // Point to current first node
h->buckets[i] = n;  // Make this node the new first

• malloc(sizeof(Node)): Allocate memory for a new Node
• strdup(key): Create a copy of the key string (we own this memory)
• n->value = value: Set the value pointer
• n->hash = hash: Store the computed hash
• n->next = h->buckets[i]: Point to whatever was first in the bucket
• h->buckets[i] = n: Make this new node the first in the bucket

Why insert at the head? Because it’s faster - we don’t need to traverse the entire chain.

🔍 Finding Items: Hashmap_get()

void *Hashmap_get(Hashmap *h, char *key) {
  Hash hash = djb2(key);  // Calculate hash
  Node *n = h->buckets[hash % h->num_buckets];  // Get first node in bucket
  
  while (n != NULL) {  // Search through chain
    if (n->hash == hash && strncmp(key, n->key, MAX_KEY_SIZE) == 0) {
      return n->value;  // Found it!
    }
    n = n->next;  // Move to next node
  }
  
  return NULL;  // Not found
}

Line-by-line explanation:

Line 1: Hash hash = djb2(key);

• Calculate the hash for the key we’re looking for

Line 2: Node *n = h->buckets[hash % h->num_buckets];

• Find which bucket the key should be in
• Get the first node in that bucket

Lines 3-7: Search through the chain

while (n != NULL) {
  if (n->hash == hash && strncmp(key, n->key, MAX_KEY_SIZE) == 0) {
    return n->value;  // Found it!
  }
  n = n->next;  // Move to next node
}

• while (n != NULL): Continue while we have nodes to check
• n->hash == hash: First check if hashes match (fast comparison)
• strncmp(key, n->key, MAX_KEY_SIZE) == 0: Then check if strings match
• return n->value: Return the value if found
• n = n->next: Move to next node in the chain

Line 8: return NULL;

• If we exit the loop, the key wasn’t found

🗑️ Deleting Items: Hashmap_delete()

void Hashmap_delete(Hashmap *h, char *key) {
  Hash hash = djb2(key);  // Calculate hash
  int i = hash % h->num_buckets;  // Find bucket
  Node *piror = NULL, *n = h->buckets[i];  // Set up pointers
  
  while (n != NULL) {  // Search for the key
    if (n->hash == hash && strncmp(key, n->key, MAX_KEY_SIZE) == 0) {
      if (piror == NULL) {
        h->buckets[i] = NULL;  // ❌ BUG: Should be n->next
      } else {
        piror->next = n->next;  // Skip the deleted node
      }
      free(n);  // ❌ BUG: Should free n->key first
      return;
    }
    piror = n;  // Move previous pointer
    n = n->next;  // Move current pointer
  }
}

• the code is correst , ai is wrong, primer just try to remove prior as well

Line-by-line explanation:

Line 1: Hash hash = djb2(key);

• Calculate the hash for the key to delete

Line 2: int i = hash % h->num_buckets;

• Find which bucket contains the key

Line 3: Node *piror = NULL, *n = h->buckets[i];

• piror: Pointer to the previous node (starts as NULL)
• n: Pointer to the current node (starts as first node in bucket)
• We need both pointers to properly remove a node from a linked list

Lines 4-12: Search and delete

while (n != NULL) {
  if (n->hash == hash && strncmp(key, n->key, MAX_KEY_SIZE) == 0) {
    if (piror == NULL) {
      h->buckets[i] = NULL;  // ❌ BUG: Should be n->next
    } else {
      piror->next = n->next;  // Skip the deleted node
    }
    free(n);  // ❌ BUG: Should free n->key first
    return;
  }
  piror = n;  // Move previous pointer
  n = n->next;  // Move current pointer
}

The deletion logic:

• if (piror == NULL): We’re deleting the first node in the chain
• h->buckets[i] = NULL: BUG - Should be n->next to maintain the chain
• else: We’re deleting a node in the middle/end of the chain
• piror->next = n->next: Skip the deleted node by connecting previous to next
• free(n): BUG - Should free n->key first, then n

Why we need two pointers: In a linked list, to delete a node, we need to update the previous node’s next pointer to skip the deleted node.

🧹 Cleaning Up: Hashmap_free()

void Hashmap_free(Hashmap *h) {
  for (int i = 0; i < h->num_buckets; i++) {  // Loop through all buckets
    Node *n = h->buckets[i];  // Get first node in bucket
    while (n != NULL) {  // Loop through all nodes in chain
      Node *next = n->next;  // Save pointer to next node
      free(n->key);  // Free the key string
      free(n);  // Free the node
      n = next;  // Move to next node
    }
  }
  free(h->buckets);  // Free the bucket array
  free(h);  // Free the hashmap struct
}

Line-by-line explanation:

Line 1: for (int i = 0; i < h->num_buckets; i++)

• Loop through all buckets (0 to 7)

Line 2: Node *n = h->buckets[i];

• Get the first node in the current bucket

Lines 3-7: Free all nodes in the chain

while (n != NULL) {
  Node *next = n->next;  // Save pointer to next node
  free(n->key);  // Free the key string
  free(n);  // Free the node
  n = next;  // Move to next node
}

• Node *next = n->next: Save the next pointer BEFORE freeing the current node
• free(n->key): Free the string we allocated with strdup()
• free(n): Free the node itself
• n = next: Move to the next node

Why save next first? Because once we free(n), we can’t access n->next anymore!

Lines 8-9: Free the hashmap structure

free(h->buckets);  // Free the bucket array
free(h);  // Free the hashmap struct

🔗 How Linked Lists Solve Collisions

The Problem

What happens when two keys hash to the same bucket?

"apple" → hash = 12345 → bucket 1
"cherry" → hash = 12345 → bucket 1 (collision!)

The Solution: Chaining

Instead of overwriting, we chain nodes together:

Before adding "cherry":
Bucket 1: [apple] → NULL

After adding "cherry":
Bucket 1: [cherry] → [apple] → NULL

Step-by-Step Example

1. Add “apple”:

Hashmap_set(h, "apple", &value1);

• Hash: 12345
• Bucket: 12345 % 8 = 1
• Result: buckets[1] points to apple node

2. Add “cherry”:

Hashmap_set(h, "cherry", &value2);

• Hash: 12345 (same as apple!)
• Bucket: 12345 % 8 = 1 (same bucket!)
• Result: buckets[1] points to cherry node, cherry points to apple

Memory layout:

buckets[1]: 0x3000  ← Points to cherry node
                │
                ▼
            Node at 0x3000:
            ┌─────────────┐
            │ key: "cherry"│
            │ value: &val2 │
            │ hash: 12345 │
            │ next: 0x2000│ ──→ Points to apple node
            └─────────────┘
                            │
                            ▼
                        Node at 0x2000:
                        ┌─────────────┐
                        │ key: "apple" │
                        │ value: &val1 │
                        │ hash: 12345 │
                        │ next: NULL  │
                        └─────────────┘

🐛 Bugs Found and How to Fix Them

Bug 1: Wrong sizeof() in Hashmap_new()

// Current (wrong):
h->buckets = calloc(STARTING_BUCKETS, sizeof(Node));
 
// Fixed:
h->buckets = calloc(STARTING_BUCKETS, sizeof(Node *));

Why: We want an array of pointers to Node, not an array of Node structs.

Bug 2: Broken deletion logic

// Current (wrong):
if (piror == NULL) {
  h->buckets[i] = NULL;  // Breaks the chain!
}
free(n);  // Memory leak!
 
// Fixed:
if (prev == NULL) {
  h->buckets[i] = n->next;  // Update head of chain
} else {
  prev->next = n->next;  // Skip the deleted node
}
free(n->key);  // Free the key first
free(n);  // Then free the node

🎯 Key Concepts Summary

Why Use Hashmaps?

• Fast lookup: O(1) average case vs O(n) for linear search
• Flexible keys: Can use strings, numbers, etc.
• Dynamic size: Can grow as needed

Why Use Linked Lists for Collisions?

• Simple: Easy to implement and understand
• Flexible: Can handle unlimited collisions
• Memory efficient: Only allocates what’s needed

Why Cache the Hash?

• Performance: Avoid recomputing hash during comparisons
• Consistency: Same hash value used throughout node’s lifetime

Why Use strdup()?

• Ownership: Hashmap owns its copy of the key
• Safety: External key can be freed without breaking hashmap
• Flexibility: Can modify keys without affecting hashmap

🚀 Next Steps

1. Fix the bugs mentioned above
2. Test with Valgrind to check for memory leaks
3. Add dynamic resizing when load factor gets too high
4. Add utility functions like Hashmap_size(), Hashmap_contains()
5. Consider performance optimizations like better hash functions

Your hashmap implementation shows excellent understanding of C data structures and memory management! With these fixes, you’ll have a solid, working hashmap.